Archive
Developers do not remember what code they have written
The size distribution of software components used in building many programs appears to follow a power law. Some researchers have and continue to do little more than fit a straight line to their measurements, while those that have proposed a process driving the behavior (e.g., information content) continue to rely on plenty of arm waving.
I have a very simple, and surprising, explanation for component size distribution following power law-like behavior; when writing new code developers ignore the surrounding context. To be a little more mathematical, I believe code written by developers has the following two statistical properties:
- nesting invariance. That is, the statistical characteristics of code sequences does not depend on how deeply nested the sequence is within
if/for/while/switchstatements, - independent of what went immediately before. That is the choice of what statement a developer writes next does not depend on the statements that precede it (alternatively there is no short range correlation).
Measurements of C source show that these two properties hold for some constructs in some circumstances (the measurements were originally made to serve a different purpose) and I have yet to see instances that significantly deviate from these properties.
How does writing code following these two properties generate a power law? The answer comes from the paper Power Laws for Monkeys Typing Randomly: The Case of Unequal Probabilities which proves that Zipf’s law like behavior (e.g., the frequency of any word used by some author is inversely proportional to its rank) would occur if the author were a monkey randomly typing on a keyboard.
To a good approximation every non-comment/blank line in a function body contains a single statement and statements do not often span multiple lines. We can view a function definition as being a sequence of statement kinds (e.g., each kind could be if/for/while/switch/assignment statement or an end-of-function terminator). The number of lines of code in a function is closely approximated by the length of this sequence.
The two statistical properties listed above allow us to treat the selection of which statement kind to write next in a function as mathematically equivalent to a monkey randomly typing on a keyboard. I am not suggesting that developers actually select statements at random, rather that the set of higher level requirements being turned into code are sufficiently different from each other that developers can and do write code having the properties listed.
Switching our unit of measurement from lines of code to number of tokens does not change much. Every statement has a few common forms that occur most of the time (e.g., most function calls contain no parameters and most assignment statements assign a scalar variable to another scalar variable) and there is a strong correlation between lines of code and token count.
What about object-oriented code, do developers follow the same pattern of behavior when creating classes? I am not aware of any set of measurements that might help answer this question, but there have been some measurements of Java that have power law-like behavior for some OO features.
The probability of encountering a given variable
If I am reading through the body of a function, what is the probability of a particular variable being the next one I encounter? A good approximation can be calculated as follows: Count the number of occurrences of all variables in the function definition up to the current point and work out the percentage occurrence for each of them, the probability of a particular variable being seen next is approximately equal to its previously seen percentage. The following graph is the evidence I give for this approximation.
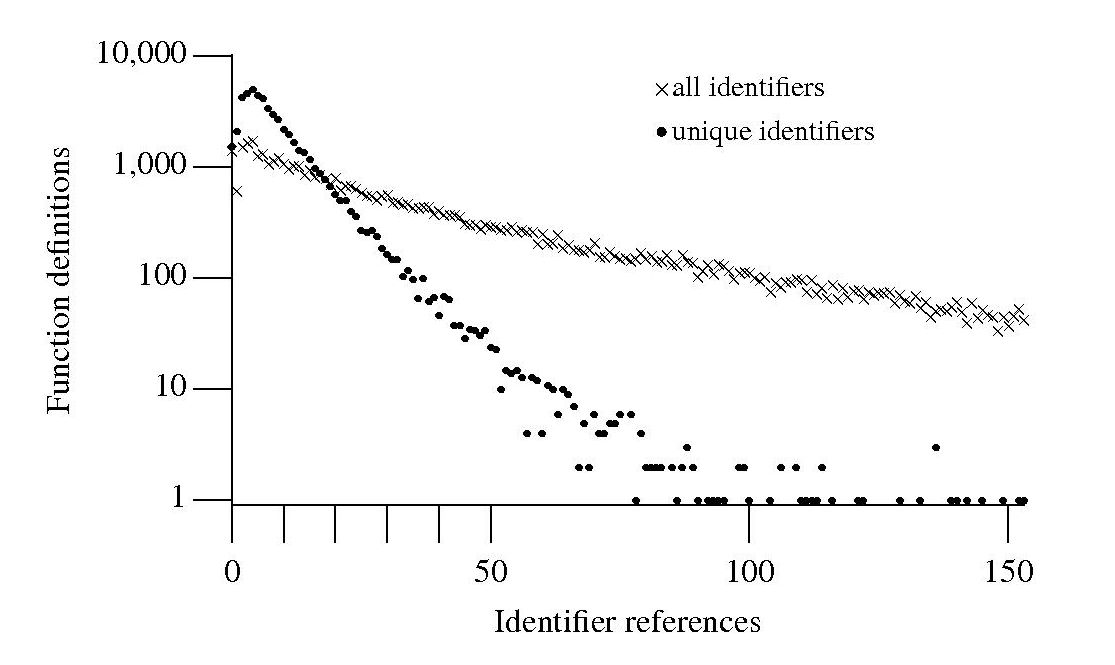
The graph shows a count of the number of C function definitions containing identifiers that are referenced a given number of times, e.g., if the identifier x is referenced five times in one function definition and ten times in another the function definition counts for five and ten are both incremented by one. That one axis is logarithmic and the bullets and crosses form almost straight lines hints that a Zipf-like distribution is involved.
There are many processes that will generate a Zipf distribution, but the one that interests me here is the process where the probability of the next occurrence of an event occurring is proportional to the probability of it having previously occurred (this includes some probability of a new event occurring; follow the link to Simon’s 1955 paper).
One can think of the value (i.e., information) held in a variable as having a given importance and it is to be expected that more important information is more likely to be operated on than less important information. This model appeals to me. Another process that will generate this distribution is that of Monkeys typing away on keyboards and while I think source code contains lots of random elements I don’t think it is that random.
The important concept here is operated on. In x := x + 1; variable x is incremented and the language used requires (or allowed) that the identifier x occur twice. In C this operation would only require one occurrence of x when expressed using the common idiom x++;. The number of occurrences of a variable needed to perform an operation on it, in a given languages, will influence the shape of the graph based on an occurrence count.
One graph does not provide conclusive evidence, but other measurements also produce straightish lines. The fact that the first few entries do not form part of an upward trend is not a problem, these variables are only accessed a few times and so might be expected to have a large deviation.
More sophisticated measurements are needed to count operations on a variable, as opposed to occurrences of it. For instance, few languages (any?) contain an indirection assignment operator (e.g., writing x ->= next; instead of x = x -> next;) and this would need to be adjusted for in a more sophisticated counting algorithm. It will also be necessary to separate out the effects of global variables, function calls and the multiple components involved in a member selection, etc.
Update: A more detailed analysis is now available.
Recent Comments