Archive
Automatically generating railroad diagrams from yacc files
Reading and understanding a language’s syntax written in the BNF-like notation used by yacc/bison takes some practice. Railroad diagrams are a much more user friendly notation, but require a lot of manual tweaking before they look as good as the following example from the json.org website:
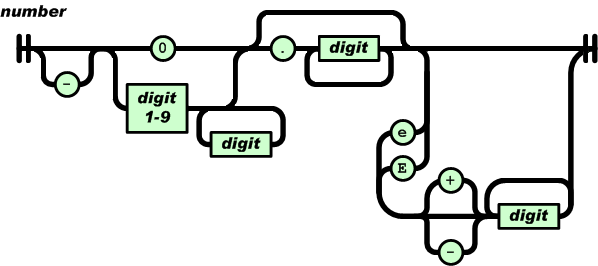
I’m currently working on a language whose syntax is evolving and I want to create a visual representation of it that can be read by non-yacc experts; spending a day of so manually creating a decent looking railroad diagram is not an efficient use of time. What automatic visualization tools are out there that I can use?
A couple of tools that look like they might produce useful results are web based (e.g., bottlecaps.de; working on an internal project for a company means I cannot take this approach). Some tools take EBNF as input (e.g., my28msec.com which is also online based); the Extensions in EBNF obviate the need for many of the low level organizational details that appear in grammars written with BNF, making grammars written using EBNF easier to layout and look good; great if I was working with EBNF. The yacc file input tools I tried (yaccviso, Vyacc) were a bit too fragile and the output was not that good.
Bison has an option to generate a output that can be processed into graphical form (using graphviz as the layout engine). Unfortunately the graphs produced are as visually tangled as the input grammar and if anything harder to follow.
It is possible to produce great looking visual diagrams using a simple tool if you are willing to spend lots of fiddling with the input grammar to control the output. I wanted to take the grammar as written (i.e., a yacc input file) and am willing to accept less than perfect output.
Most of the syntax rules in a yacc grammar are straight forward sequences of tokens that have an obvious one-to-one mapping and there are a few commonly seen idioms. I decided to write a tool that concentrated on untangling the idioms and let the simple stuff look after itself. One idiom that has a visual representation very different from its yacc form is the two productions used to specify an arbitrary long list, e.g., a semicolon separated list of ys is often written as (ok, there might perhaps be times when right recursion is appropriate):
x : y | x ";" y ; |
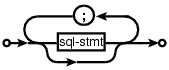
and I wanted something that looked like (from the sql-lite web site, which goes one better and allows support for the list to be optional:
Graph layout is a complicated business and like everybody else I decided to use graphviz to do the heavy lifting (specifically I would generate the layout directives used by dot). All I had to do was write a yacc grammar to dot translator (and not spend lots of time doing it).
The dot language provides a directives that specify the visual properties of nodes and the connections between them. For instance:
n_0[shape=point] n_1[label="sql-stmt"] n_2[label=";"] n_3[shape=point] n_0 -> n_3 n_0 -> n_1 n_1 -> n_3 n_1 -> n_2 n_2 -> n_1 |
is the dot specification of the optional semicolon separated list of sql-stmts displayed above.
Dot takes a list of directives describing the nodes and edges of a graph and makes its own decisions about how to layout the output. It is possible to specify in excruciating detail exactly how to do the layout, but I wanted everything to be automated.
I decided to write the tool in awk because it has great input token handling facilities and I use it often enough to be fluent.
Each grammar rule containing one or more productions is mapped to a single graph. When generating postscript dot puts each graph on a separate page, other output formats appear to loose all but one of the graphs. To make sure each rule fitted on a page I had the text point size depend on the number of productions in a rule, more productions smaller point size. The most common idioms are handled (i.e., list-of and optional construct) with hooks available to handle others. Productions within a rule will often have common token sequences but the current version only checks for matching token sequences at the start of a production and all productions in a rule have to start with the same sequence. Words written all in upper-case are assumed to be language tokens and are converted to lower case and bracketed with quotes. The 300+ lines of conversion tool’s awk source is available for download.
The follow examples are taken from an attempted yacc grammar of C++ done when people still thought such a thing could be created. While the output does have a certain railroad diagram feel to it, the terrain must be very hilly to generate those curvaceous lines.
and the run of the mill rules look good, a C++ primary-expression is:
and we can rely on C++ to push syntax rule complexity to the limit, a postfix-expression is:
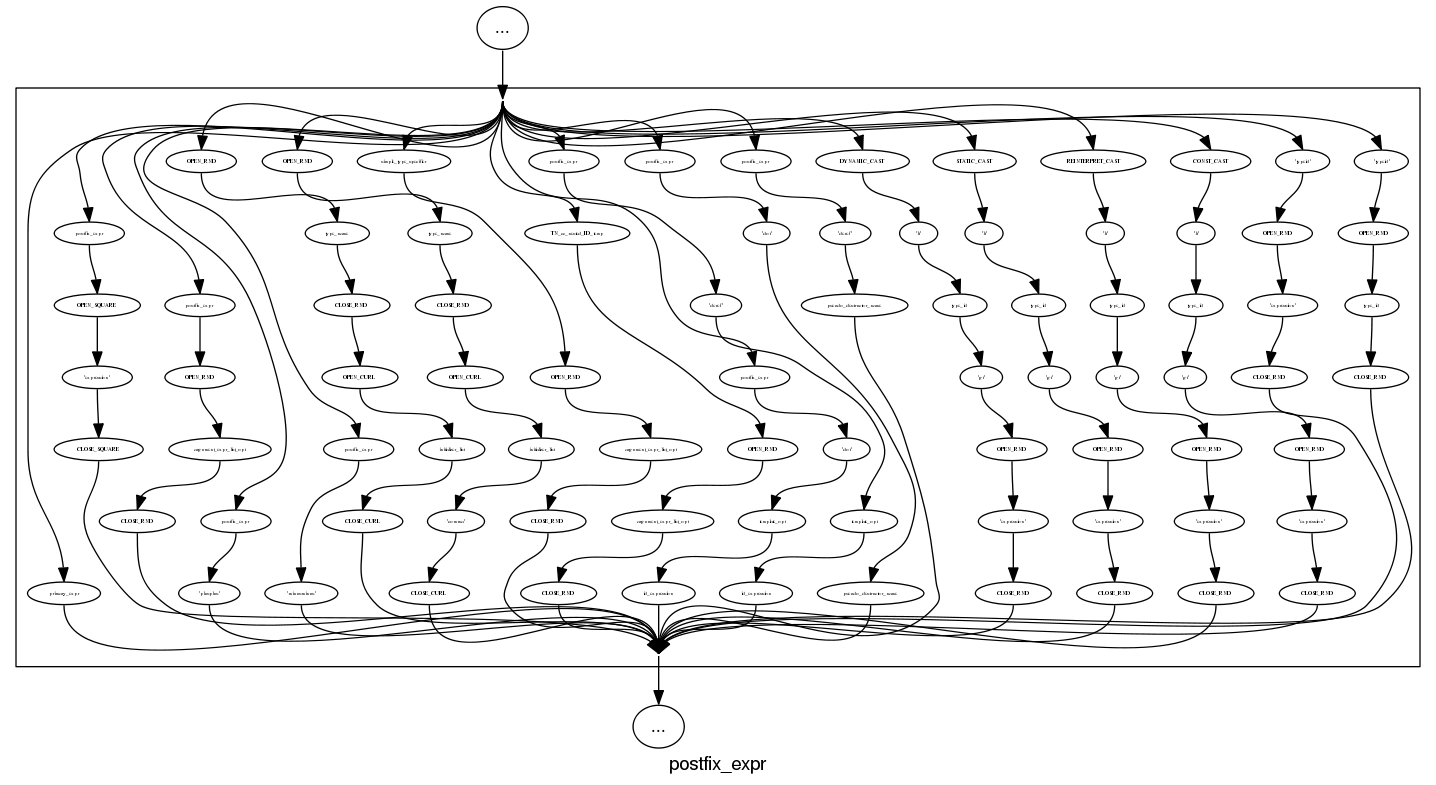
What about the idioms? A simple list of items looks good:
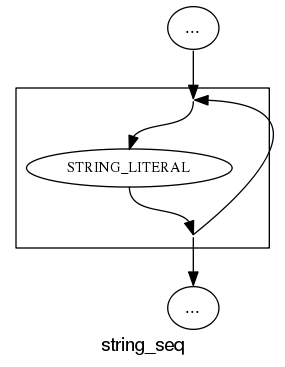
and slightly less good when separators are involved:
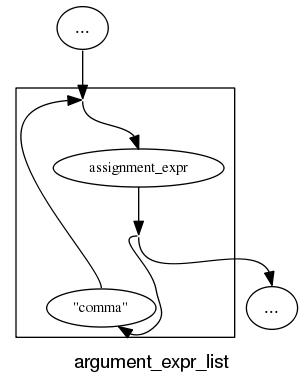
and if we push our luck things start to look tangled:
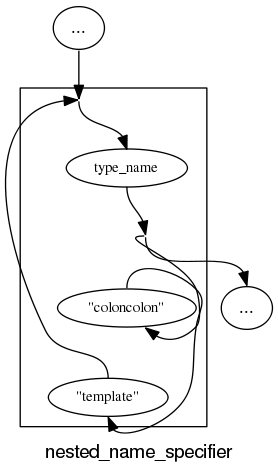
With a bit more work invested on merging token sequences common to two or more rules the following might look a lot less cluttered:
Apart from a few tangled cases the results are not bad for a tool that was a few hours work. I will wait a bit to see if the people I deal with find this visual form of use.
In the meantime I would be interested to hear about my readers experience with visualizing grammars, using dot to this kind of thing and any suggestions they have. As a long time user of dot I know that there are lots of ways of influencing the final layout (e.g., changing the ordering or edges and nodes in its input), I will have to be careful not to get pulled down this rabbit hole.
Parsing R code: Freedom of expression is not always a good idea
With my growing interest in R it was inevitable that I would end up writing a parser for it. The fact that the language is relatively small (the add-on packages do the serious work) hastened the event because it did not look like much work; famous last words. I knew about R’s design and implementation being strongly influenced by the world view of functional programming and this should have set alarm bells ringing; this community have a history of willfully ignoring some of the undesirable consequences of their penchant of taking simple ideas and over generalizing them (i.e., I should have expected hidden complications).
While the official R language definition only contains a tiny fraction of the information needed to create a full implementation I decided to use it rather than ‘cheat’ and look at the R project implementation sources. I took as my oracle of correctness the source code of the substantial amount of R in its 3,000+ package library. This approach would help me uncover some of the incorrect preconceived ideas I have about how R source fits together.
I started with a C lexer and chopped and changed (it is difficult to do decent error recovery in automatically generated lexers and I prefer to avoid them). A few surprises cropped up ** is supported as an undocumented form of ^ and by default ]] must be treated as two tokens (e.g., two ] in a[b[c]] but one ]] in d[[e]], an exception to the very commonly used maximal munch rule).
The R grammar is all about expressions with some statement bits and pieces thrown in. R operator precedence follows that of Fortran, except the precedence of unary plus/minus has been increased to be above multiply/divide (instead of below). Easy peasy, cut and paste an existing expression grammar and done by tea time :-). Several tea times later I have a grammar that parses all of the R packages (apart from 80+ real syntax errors contained therein and a hand full of kinky operator combinations I’m not willing to contort the grammar to support). So what happened?
Two factors accounts for most of the difference between my estimate of the work required and the actual work required:
- my belief that a well written grammar has no ambiguities (while zero is a common goal for many projects a handful might be acceptable if the building is on fire and I have to leave). A major advantage of automatic generation of parser tables from a grammar specification is being warned about ambiguities in the grammar (either shift/reduce or reduce/reduce conflicts). At an early stage I was pulling my hair out over having 59 conflicts and decided to relent and look at the R project source and was amazed to find their grammar has 81 ambiguities!
I have managed to get the number of ambiguities down to the mid-30s, not good at all but it will have to do for the time being.
- some of my preconceptions about of how R syntax worked were seriously wrong. In some cases I spotted my mistake quickly because I recognized the behavior from other languages I know, other misconceptions took a lot longer to understand and handle because I did not believe anybody would design expression evaluation to work that way.
The root cause of the difference can more concretely be traced to the approach to specifying language syntax. The R project grammar is written using the form commonly seen in functional language implementations and introductory compiler books. This form has the advantage of being very short and apparently simple; the following is a cut down example in a form of BNF used by many parser generators:
expr : expr op expr | IDENTIFIER ; op : &' | '==' | '>' | '+' | '-' | '*' | '/' | '^' ; |
This specifies a sequence of IDENTIFIERs separated by binary operators and is ambiguous when the expression contains more than two operators, e.g., a + b * c can be parsed in more than one way. Parser generators such as Yacc will complain and flag any ambiguity and pick one of the possibilities as the default behavior for handling a given ambiguity; developers can specify additional grammar information in the file read by Yacc to guide its behavior when deciding how to resolve specific ambiguities. For instance, the relative precedence of operators can be specified and this information would be used by Yacc to decide that the ambiguous expression a + b * c should be parsed as-if it had been written like a + (b * c) rather than like (a + b) * c. The R project grammar is short, highly ambiguous and relies on the information contained in the explicitly specified relative operator precedence and associativity directives to resolve the ambiguities.
An alternative method of specifying the grammar is to have a separate list of grammar rules for each level of precedence (I always use this approach). In this approach there is no ambiguity, the precedence and associativity are implicitly specified by how the grammar is written. Obviously this approach creates much longer grammars, there will be at least two rules for every precedence level (19 in R, many with multiple operators). The following is a cut down example containing just multiple, divide, add and subtract:
... multiplicative_expression: cast_expression | multiplicative_expression '*' cast_expression | multiplicative_expression '/' cast_expression ; additive_expression: multiplicative_expression | additive_expression '+' multiplicative_expression | additive_expression '-' multiplicative_expression ; ... |
The advantages of this approach are that, because there are no ambiguities, the developer can see exactly how the grammar behaves and if an ambiguity is accidentally introduced when editing the source it should be noticed when the parser generator reports a problem where previously there were none (rather than the new ambiguity being hidden in the barrage of existing ones that are ignored because they are so numerous).
My first big misconception about R syntax was to think that R had statements, it doesn’t. What other languages would treat as statements R always treats as expressions. The if, for and while constructs have values (e.g., 2*(if (x == y) 2 else 4)). No problem, I used Algol 68 as an undergraduate, which supports this kind of usage. I assumed that when an if appeared as an operand in an expression it would have to be bracketed using () or {} to avoid creating a substantial number of parsing ambiguities; WRONG. No brackets need be specified, the R expression if (x == y) 2 else 4+1 is ambiguous (it could be treated as-if it had been written if (x == y) 2 else (4+1) or (if (x == y) 2 else 4)+1) and the R project grammar relies on its precedence specification to resolve the conflict (in favor of the first possibility listed above).
My next big surprise came from the handling of unary operators. Most modern languages give all unary operators the same precedence, generally higher than any binary operator. Following Fortran the R unary operators have a variety of different precedence levels; however R did not adopt the restrictions Fortran places on where unary operators can occur.
I assumed that R had adopted the restrictions used by other languages containing unary operators at different precedence levels, e.g., not allowing a unary operator token to follow a binary operator token (i.e., there has to be an intervening opening parenthesis); WRONG. R allows me to write 1 == !1 < 0, while Fortran (and Ada, etc) require that a parenthesis be inserted between the operands == ! (hopefully resulting in the intent being clearer).
I had to think a bit to come up with an explicit set of grammar rules to handle R unary operator's freedom of expression (without creating any ambiguities).
Stepping back from the details. My view is that programming language syntax should be designed to reduce the number of mistakes developers make. Requiring that brackets appear in certain contexts helps prevent mistakes by the original author and subsequent readers of the code.
Claims that R (or any other language) syntax is 'natural' is clearly spurious and really no more than a statement of preference by the speaker. Our DNA has not yet been found to equip us to handle one programming language better than another.
Over the coming months I hope to have the time to analyse R source looking for faults that might not have occurred had brackets been used. Also how much code might be broken if R started to require brackets in certain contexts?
An example of the difference that brackets can make is provided by the handling of the unary ! operator in R and C/C++/Java/etc. Take the expression !x > y, which R parses as-if written !(x > y) and C/C++/Java/etc as if written (!x) > y. I would not claim that either is better than the other from the point of view of developers getting the behavior right, I know that some C programmers get it wrong and I suspect that some R programmers do too.
By increasing the precedence of unary plus/minus the R designers ensured that 8/-2/2 was parsed like (8/-2)/2 rather than 8/(-2/2).
Recent Comments