Archive
Changes in the API/non-API method call ratio with program size
Amount of code is the fundamental metric of software engineering. How do things change as the amount of code changes and often just as interestingly what does not change with code size?
Most languages include some kind of base library functionality. Languages such as Java and C++ not only include a very large library but also a huge, widely used, collection of third-party libraries.
Let’s count every method call in lots of Java programs and for each program divide these calls into two groups, calls to methods in well-known libraries (call these the API methods) and all other method calls (i.e., calls to methods written by the developers who wrote each of the programs measured; call these the non-API methods).
I would expect the ratio of API to non-API method calls to be independent of program size.
Yes, the number of possible different API calls is fixed while the number of possible non-API calls increases with program size, but I don’t see why a changing ratio of unique calls should change the ratio of total calls.
Yes, larger programs are likely to contain more architectural stuff whose code is more likely to contain calls to non-API methods, but the percentage of architectural code is very small and unlikely to have much impact on the overall numbers.
The authors of the paper: Large-scale, AST-based API-usage analysis of open-source Java projects made their data available and so I got to check out my thinking 🙂
The plot below shows everything going to plan until around 10,000 method calls (about 50,000 lines of code). Why that sudden kink in the line (code and data)?
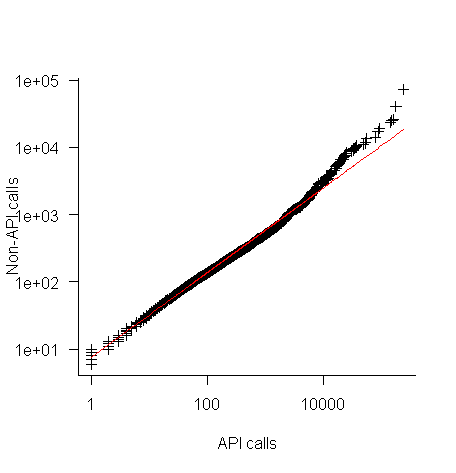
One possibility is that once a program gets to a size of around 50,000 lines the developers decide to invest in one or more wrapper packages which create a purpose built interface to an API (programs often have their own requirements and needs that existing an existing API interface does not quite meet); this would cause API calls to decrease and non-API calls to increase. If this pattern of usage occurred there would be a permanent change in the API/non-API ratio, and in practice the ratio change appears to be temporary.
I’m a bit stumped by this behavior. Suggestions on possible mechanisms welcome.
I wish I had the time to investigate, but I have a book to finish.
Benford’s law and numeric literals in source code
Benford’s law applies to values derived from a surprising number number of natural and man-made processes. I was very optimistic that it would also apply to numeric literals in source code. Measurements of C source showed that I was wrong (the chi-square fit was 1,680 for decimal integer literals and 132,398 for floating literals).
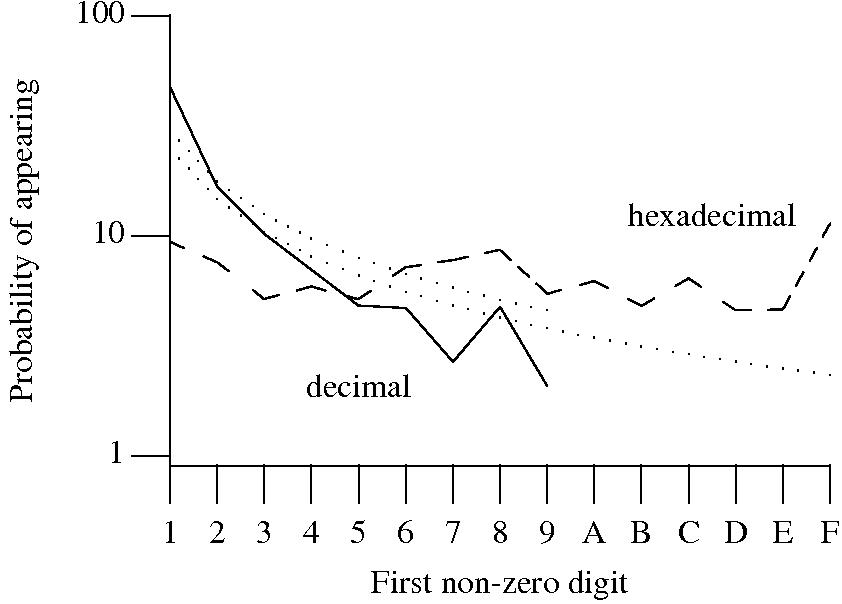
Probability that the leading digit of an (decimal or hexadecimal) integer literal has a particular value (dotted lines predicted by Benford’s law).
What are the conditions necessary for a sample of values to follow Benford’s law? A number of circumstances have been found to result in sample values having a leading digit that follows Benford’s law, including:
Samples that have been found to follow Benford’s law include lists of physical constants and accounting data (so much so that it has been used to detect accounting fraud). However, the number of data-sets containing values whose leading digit follows Benford’s law is not a great as some would make us believe.
Why don’t the leading digits of numeric literals in source code follow Benford’s law?
++/-- operators reduces the number of instances of 1 to increment/decrement a value). But this only applies to integer types, not floating types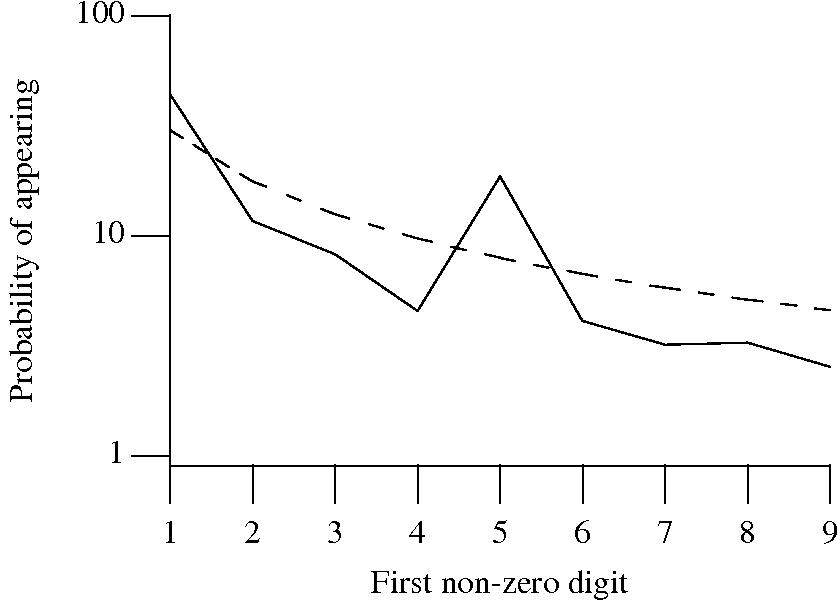
Probability that the leading, first non-zero, digit of a floating literal has a particular value (dashed line predicted by Benford’s law).
5 for the floating-point literals? Have values been rounded to produce 0.5? This looks like an area where methods used for accounting fraud detection might be applied (not that any fraud is implied, just irregularity).These surprising measurements show that there is a lot to the shape of numeric literals that is yet to be discovered.
Recent Comments