Archive
Initial impressions of RangeLab
I was rummaging around in the source of R looking for trouble, as one does, when I came across what I believed to be a less than optimally accurate floating-point algorithm (function R_pos_di in src/main/arithemtic.c). Analyzing the accuracy of floating-point code is notoriously difficult and those having the required skills tend to concentrate their efforts on what are considered to be important questions. I recently discovered RangeLab, a tool that seemed to be offering painless floating-point code accuracy analysis; here was an opportunity to try it out.
Installation went as smoothly as newly released personal tools usually do (i.e., some minor manual editing of Makefiles and a couple of tweaks to the source to comment out function calls causing link errors {mpfr_random and mpfr_random2}).
RangeLab works by analyzing the flow of values through a program to produce the set of output values and the error bounds on those values. Input values can be specified as a range, e.g., f = [1.0, 10.0] says f can contain any value between 1.0 and 10.0.
My first RangeLab program mimicked the behavior of the existing code in R_pos_di:
n=-10; f=[1.0, 10.0]; res = 1.0; if n < 0, n = -n; f = 1 / f; end while n ~= 0, if (n / 2)*2 ~= n, res = res * f; end n = n / 2; if n ~= 0, f = f*f; end end |
and told me that the possible range of values of res was:
res ans = float64: [1.000000000000001E-10,1.000000000000000E0] error: [-2.109423746787798E-15,2.109423746787799E-15] |
Changing the code to perform the divide last, rather than first, when the exponent is negative:
n=-10; f=[1.0, 10.0]; res = 1.0; is_neg = 0; if n < 0, n = -n; is_neg = 1 end while n ~= 0, if (n / 2)*2 ~= n, res = res * f end n = n / 2; if n ~= 0, f = f*f end if is_neg == 1, res = 1 / res end end |
and the error in res is now:
res ans = float64: [1.000000000000000E-10,1.000000000000000E0] error: [-1.110223024625156E-16,1.110223024625157E-16] |
Yea! My hunch was correct, moving the divide from first to last reduces the error in the result. I have reported this code as a bug in R and wait to see what the R team think.
Was the analysis really that painless? The Rangelab language is somewhat quirky for no obvious reason (e.g., why use ~= when everybody uses != these days and if conditionals must be followed by a character why not use the colon like Python does?) It would be real useful to be able to cut and paste C/C++/etc and only have to make minor changes.
I get the impression that all the effort went into getting the analysis correct and user interface stuff was a very distant second. This is the right approach to take on a research project. For some software to make the leap from interesting research idea to useful tool it is important to pay some attention to the user interface.
The current release does not deserve to be called 1.0 and unless you have an urgent need I would suggest waiting until the usability has been improved (e.g., error messages give some hint about what is wrong and a rough indication of which line the problem occurs on).
RangeLab has shown that there is simpler method of performing useful floating-point error analysis. With some usability improvements RangeLab would be an essential tool for any developer writing code involving floating-point types.
Update: The R team, in the form of Martin Maechler, resolved my report in just over 14 hours! The function R_pos_di is not called, the pow function from the C library (which takes two double arguments rather than a double and an int) has been found to be more accurate. Martin says this usage is not less accurate even for n=3, which I find surprising; I agree it should be more accurate for large values of n.
pow is one of the more complicated maths functions, involving finding a log, a multiply and then returning the exponent of this result. There are lots of boundary values that need to be checked and the code goes on for a while. I will wait for the usability of RangeLab to improve before attempting to compare its accuracy against the simpler algorithm for integer powers. Looking at the SunOracle library sources, if both arguments have integral values the ‘integer power’ algorithm is used (with the divide performed last).
Optimizing floating-point expressions for accuracy
Floating-point arithmetic is one topic that most compiler writers tend to avoid as much as possible. The majority of programs don’t use floating-point (i.e., low customer demand), much of the analysis depends on the range of values being operated on (i.e., information not usually available to the compiler) and a lot of developers don’t understand numerical methods (i.e., keep the compiler out of the blame firing line by generating code that looks like what appears in the source).
There is a scientific and engineering community whose software contains lots of floating-point arithmetic, the so called number-crunchers. While this community is relatively small, many of the problems it works on attract lots of funding and some of this money filters down to compiler development. However, the fancy optimizations that appear in these Fortran compilers (until the second edition of the C standard in 1999 Fortran did a much better job of handling the minutia of floating-point arithmetic) are mostly about figuring out how to distribute the execution of loops over multiple functional units (i.e., concurrent execution).
The elephant in the floating-point evaluation room is result accuracy. Compiler writers know they have to be careful not to throw away accuracy (e.g., optimizing out what appear to be redundant operations in the Kahan summation algorithm), but until recently nobody had any idea how to go about improving the accuracy of what had been written. In retrospect one accuracy improvement algorithm is obvious, try lots of possible combinations of the ways in which an expression can be written and pick the most accurate.
There are lots of ways in which the operands in an expression can be paired together to be operated on; some of the ways of pairing the operands in a+b+c+d include (a+b)+(c+d), a+(b+(c+d)) and (d+a)+(b+c) (unless the source explicitly includes parenthesis compilers for C, C++, Fortran and many other languages (not Java which is strictly left to right) are permitted to choose the pairing and order of evaluation). For n operands (assuming the operators have the same precedence and are commutative) the number is combinations is 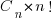 where
where 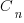 is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands
is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands 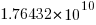 of which
of which 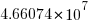 are unique.
are unique.
A recent study by Langlois, Martel and Thévenoux analysed the accuracy achieved by all unique permutations of ten operands on four different data sets. People within the same umbrella project are now working on integrating this kind of analysis into a compiler. This work is another example of the growing trend in compiler research of using the processing power provided by multiple cores to use algorithms that were previously unrealistic.
Over the last six years or so there has been lot of very interesting floating-point work going on in France, with gcc and llvm making use of the MPFR library (multiple-precision floating-point) for quite a while. Something very new and interesting is RangeLab which, given the lower/upper bounds of each input variable to a program (a simple C-like language) computes the range of the outputs as well as ranges for the roundoff errors (the tool assumes IEEE floating-point arithmetic). I now know that over the range [800, 1000] the expression x*(x+1) is a lot more accurate than x*x+x.
Update: See comment from @Eric and my response below.
Recent Comments