Archive
Perturbed expressions may ‘recover’
This week I have been investigating the impact of perturbing the evaluation of random floating-point expressions. In particular, the impact of adding 1 (and larger values) at a random point in an expression containing many binary operators (simply some combination of add/multiply).
What mechanisms make it possible for the evaluation of an expression to be unchanged by a perturbation of +1.0 (and much larger values)? There are two possible mechanisms:
- the evaluated value at the perturbation point is ‘watered down’ by subsequent operations, such that the original perturbed value makes no contribution to the final result. For instance, the IEEE single precision float mantissa is capable of representing 6-significant digits; starting with, say, the value
0.23, perturbing by adding1.0gives1.23, followed by a sequence of many multiplications by values between zero and one could produce, say, the value6.7e-8, which when added to, say,0.45, gives0.45, i.e., the perturbed value is too small to affect the result of the add, - the perturbed branch of the expression evaluation is eventually multiplied by zero (either because the evaluation of the other branch produces zero, or the operand happens to be zero). The exponent of an IEEE single precision float can represent values as small as
1e-38, before underflowing to zero (ignoring subnormals); something that is likely to require many more multiplies than required to lose 6-significant digits.
The impact of a perturbation disappears when its value is involved in a sufficiently long sequence of repeated multiplications.
The probability that the evaluation of a sequence of  multiplications of random values uniformly distributed between zero and one produces a result less than
multiplications of random values uniformly distributed between zero and one produces a result less than  is given by
is given by 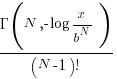 , where
, where 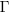 is the incomplete gamma function, and
is the incomplete gamma function, and  is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various
is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various  (code):
(code):
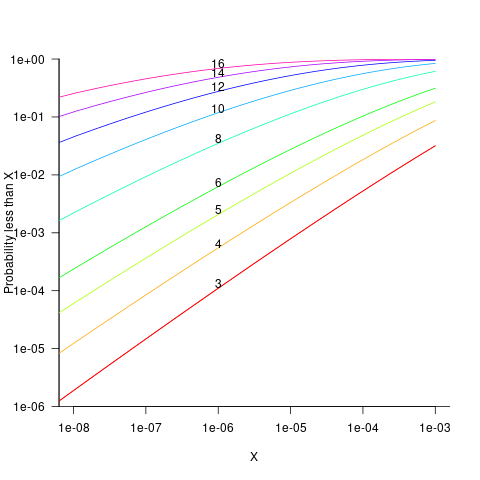
Looking at this plot, a sequence of 10 multiplications has around a 1-in-10 chance of evaluating to a value less than 1e-6.
In practice, the presence of add operations will increase the range of operands values to be greater than one. The expected distribution of result values for expressions containing various percentages of add/multiply operators is covered in an earlier post.
The probability that the evaluation of an expression involves a sequence of  multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of
multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of  operands is proportional to
operands is proportional to 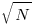 .
.
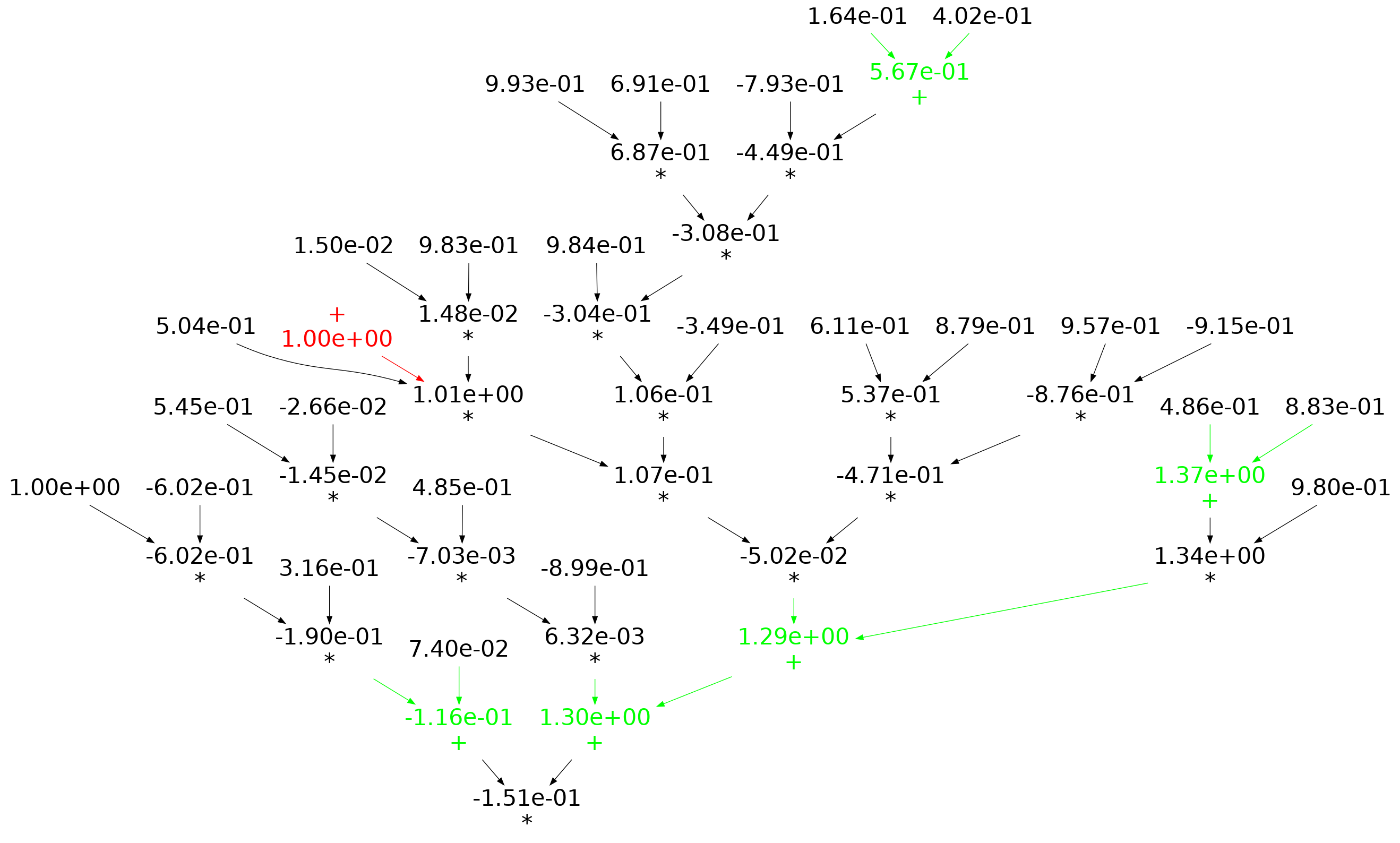
When an expression has a ‘bushy’ balanced form, there are many relatively distinct evaluation paths, the expected number of operations along a path is proportional to 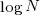 . The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
. The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
When an expression has a ‘tall’ form, there is one long evaluation path, with a few short paths hanging off it, the expected number of operations along the long path is proportional to  . The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
. The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):

If, one by one, the result of every operator in an expression is systematically perturbed (by adding some value to it), it is known that in some cases the value of the perturbed expression is the same as the original.
The following results were obtained by generating 200 random C expressions containing some percentage of add/multiply, some number of operands (i.e., 25, 50, 75, 100, 150), one-by-one perturbing every operator in every expression, and comparing the perturbed result value to the original value. This process was repeated 200 times, each time randomly selecting operand values from a uniform distribution between -1 and 1. The perturbation values used were: 1e0, 1e2, 1e4, 1e8, 1e16. A 32-bit float type was used throughout.
Depending on the shape of the expression tree, with 80% multiplications and 100 operands, the fraction of perturbed expressions returning an unchanged value can vary from 1% to 40%.
The regression model fitted to the fraction of unchanged expressions contains lots of interactions (the simple version is that the fraction unchanged increases with more multiplications, decreases as the log of the perturbation value, the square root of the number of operands is involved; code+data):
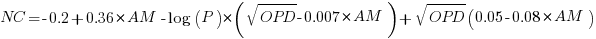
where: 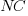 is the fraction of perturbed expressions returning the original value,
is the fraction of perturbed expressions returning the original value, 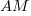 the percentage of add operators (not multiply),
the percentage of add operators (not multiply), 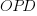 the number of operands in the expression, and
the number of operands in the expression, and 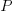 the perturbation value.
the perturbation value.
There is a strong interaction with the shape of the expression tree, but I have not found a way of integrating this into the model.
The following plot shows the fraction of expressions unchanged by adding one, as the perturbation point moves up a tall tree, x-axis, for expressions containing 50 and 100 operands, and various percentages of multiplications (code+data):
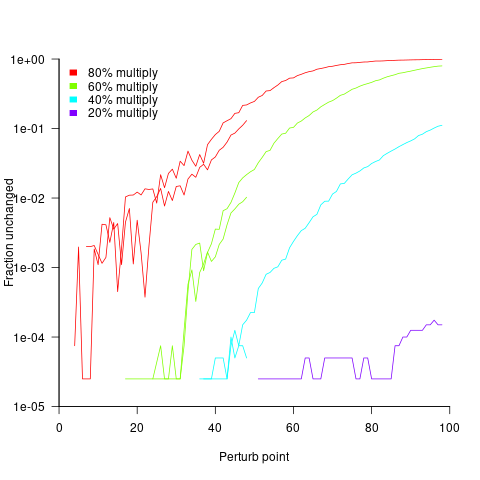
No attempt was made to count the number of expression evaluations where the perturbed value was eventually multiplied by zero (the second bullet point discussed at the start).
Distribution of add/multiply expression values
The implementation of scientific/engineering applications requires evaluating many expressions, and can involve billions of adds and multiplies (divides tend to be much less common).
Input values percolate through an application, as it is executed. What impact does the form of the expressions evaluated have on the shape of the output distribution; in particular: What is the distribution of the result of an expression involving many adds and multiplies?
The number of possible combinations of add/multiply grows rapidly with the number of operands (faster than the rate of growth of the Catalan numbers). For instance, given the four interchangeable variables: w, x, y, z, the following distinct expressions are possible: w+x+y+z, w*x+y+z, w*(x+y)+z, w*(x+y+z), w*x*y+z, w*x*(y+z), w*x*y*z, and w*x+y*z.
Obtaining an analytic solution seems very impractical. Perhaps it’s possible to obtain a good enough idea of the form of the distribution by sampling a subset of calculations, i.e., the output from plugging random values into a large enough sample of possible expressions.
What is needed is a method for generating random expressions containing a given number of operands, along with a random selection of add/multiply binary operators, then to evaluate these expressions with random values assigned to each operand.
The approach I used was to generate C code, and compile it, along with the support code needed for plugging in operand values (code+data).
A simple method of generating postfix expressions is to first generate operations for a stack machine, followed by mapping this to infix form to a postfix form.
The following awk generates code of the form (‘executing’ binary operators, o, right to left): o v o v v. The number of variables in an expression, and number of lines to generate, are given on the command line:
# Build right to left function addvar() { num_vars++ cur_vars++ expr="v " expr # choose variable later } function addoperator() { cur_vars-- expr="o " expr # choose operator later } function genexpr(total_vars) { cur_vars=2 num_vars=2 expr="v v" # Need two variables on stack while (num_vars <= total_vars) { if (cur_vars == 1) # Must push a variable addvar() else if (rand() > 0.2) # Seems to produce reasonable expressions addvar() else addoperator() } while (cur_vars > 1) # Add operators to use up operands addoperator() print expr } BEGIN { # NEXPR and VARS are command line options to awk if (NEXPR != "") num_expr=NEXPR else num_expr=10 for (e=1; e <=num_expr; e++) genexpr(VARS) } |
the following awk code maps each line of previously generated stack machine code to a C expression, wraps them in a function, and defines the appropriate variables.
function eval(tnum) { if ($tnum == "o") { printf("(") tnum=eval(tnum+1) #recurse for lhs if (rand() <= PLUSMUL) # default 0.5 printf("+") else printf("*") tnum=eval(tnum) #recurse for rhs printf(")") } else { tnum++ printf("v[%d]", numvars) numvars++ # C is zero based } return tnum } BEGIN { numexpr=0 print "expr_type R[], v[];" print "void eval_expr()" print "{" } { numvars=0 printf("R[%d] = ", numexpr) numexpr++ # C is zero based eval(1) printf(";\n") next } END { # print "return(NULL)" printf("}\n\n\n") printf("#define NUMVARS %d\n", numvars) printf("#define NUMEXPR %d\n", numexpr) printf("expr_type R[NUMEXPR], v[NUMVARS];\n") } |
The following is an example of a generated expression containing 100 operands (the array v is filled with random values):
R[0] = ((((((((((((((((((((((((((((((((((((((((((((((((( ((((((((((((((((((((((((v[0]*v[1])*v[2])+(v[3]*(((v[4]* v[5])*(v[6]+v[7]))+v[8])))*v[9])+v[10])*v[11])*(v[12]* v[13]))+v[14])+(v[15]*(v[16]*v[17])))*v[18])+v[19])+v[20])* v[21])*v[22])+(v[23]*v[24]))+(v[25]*v[26]))*(v[27]+v[28]))* v[29])*v[30])+(v[31]*v[32]))+v[33])*(v[34]*v[35]))*(((v[36]+ v[37])*v[38])*v[39]))+v[40])*v[41])*v[42])+v[43])+ v[44])*(v[45]*v[46]))*v[47])+v[48])*v[49])+v[50])+(v[51]* v[52]))+v[53])+(v[54]*v[55]))*v[56])*v[57])+v[58])+(v[59]* v[60]))*v[61])+(v[62]+v[63]))*v[64])+(v[65]+v[66]))+v[67])* v[68])*v[69])+v[70])*(v[71]*(v[72]*v[73])))*v[74])+v[75])+ v[76])+v[77])+v[78])+v[79])+v[80])+v[81])+((v[82]*v[83])+ v[84]))*v[85])+v[86])*v[87])+v[88])+v[89])*(v[90]+v[91])) v[92])*v[93])*v[94])+v[95])*v[96])*v[97])+v[98])+v[99])*v[100]); |
The result of each generated expression is collected in an array, i.e., R[0], R[1], R[2], etc.
How many expressions are enough to be a representative sample of the vast number that are possible? I picked 250. My concern was the C compilers code generator (I used gcc); the greater the number of expressions, the greater the chance of encountering a compiler bug.
How many times should each expression be evaluated using a different random selection of operand values? I picked 10,000 because it was a big number that did not slow my iterative trial-and-error tinkering.
The values of the operands were randomly drawn from a uniform distribution between -1 and 1.
What did I learn?
- Varying the number of operands in the expression, from 25 to 200, had little impact on the distribution of calculated values.
- Varying the form of the expression tree, from wide to deep, had little impact on the distribution of calculated values.
- Varying the relative percentage of add/multiply operators had a noticeable impact on the distribution of calculated values. The plot below shows the number of expressions (binned by rounding the absolute value to three digits) having a given value (the power law exponents fitted over the range 0 to 1 are: -0.86, -0.61, -0.36; code+data):
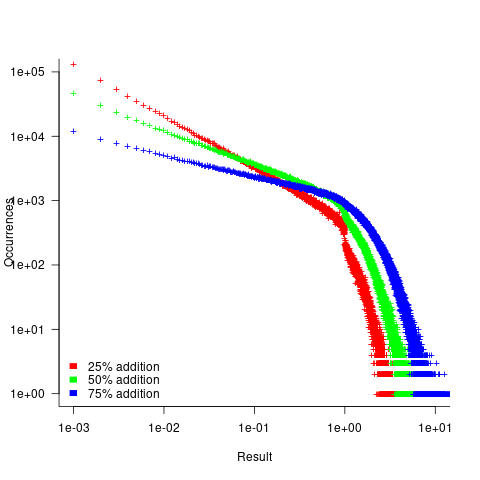
A rationale for the change in the slopes, for expressions containing different percentages of add/multiply, can be found in an earlier post looking at the distribution of many additions (the Irwin-Hall distribution, which tends to a Normal distribution), and many multiplications (integer power of a log).
- The result of many additions is to produce values that increase with the number of additions, and spread out (i.e., increasing variance).
- The result of many multiplications is to produce values that become smaller with the number of multiplications, and become less spread out.
Which recent application spends a huge amount of time adding/multiplying values in the range -1 to 1?
Large language models. Yes, under the hood they are all linear algebra; adding and multiplying large matrices.
LLM expressions are often evaluated using a half-precision floating-point type. In this 16-bit type, the exponent is biased towards supporting very small values, at the expense of larger values not being representable. While operations on a 10-bit significand will experience lots of quantization error, I suspect that the behavior seen above not noticeable change.
Unique values generated by expressions of a given complexity
The majority of integer constants appearing in source code can be represented using a few bits. CPU designers use this characteristic when designing instruction sets, creating so called short-form or quick instructions that perform some operation involving small integer values, e.g., adding a value between 1 and 8 to a register. Writers of code optimizers are always looking for sequences of short-form instructions that are faster/smaller than the longer forms (the INMOS Transputer only had a short form for load immediate).
I have recently been looking at optimizing expressions written for a virtual machine that only supports immediate loads of decimal values between 1 an 9, and binary add/subtract/multiply/divide, e.g., optimizing an expression containing four operators, ((2*7)+9)*4+9 which evaluates to 101, to one containing three operators, (8+9)*6-1 also evaluates to 101. Intermediate results can have fractional values, but I am only interested in expressions whose final result has an integer value (i.e., zero fractional part).
A little thought shows that the value of an expression containing a subexpression whose value includes a fractional value (e.g., 1/3) can always be generated by an expression containing the same or a fewer number of operators and no intermediate fractional value intermediate results (e.g., 9/(1/5) can be generated using 9*5, i.e., the result of any divide operation always has to be an integer if the final result is to be a unique integer. Enumerating the unique set of values generated by expressions containing a given number of operators shows that divide is redundant for expressions containing six of fewer operators and only adds 11 unique values for seven operators (379,073 possibilities without divide)
Removing support for the minus operator only reduces the size of the result set by around 10%. Possibly being worthwhile time saving for expressions containing many operators or searching for an expression whose result value is very large.
There does not appear to be a straightforward (and fast) algorithm that returns the minimal operation expression for a given constant.
I wrote an R program to exhaustively generate all integer values returned by expressions containing up to seven operators. To find out how many different values, integer/real, could be calculated I wrote a maxima program (this represents fractional values using a rational number representation and exceeds 4G byte of storage for expressions containing more than five operators).
The following figure shows the number of different values that can be generated by an expression containing a given number of operators (blue), the number of integer values (black), the number of positive integer values (red), the smallest positive integer that cannot be calculated by an expression containing the given number of operators (green) (circles are for add/subtract/multiply/divide, squares for add/multiply). Any value below a green line is guaranteed to have a solution in the in the given number of operators (or fewer). The blue diamond line is the mean value of a random expression containing the given number of operators.
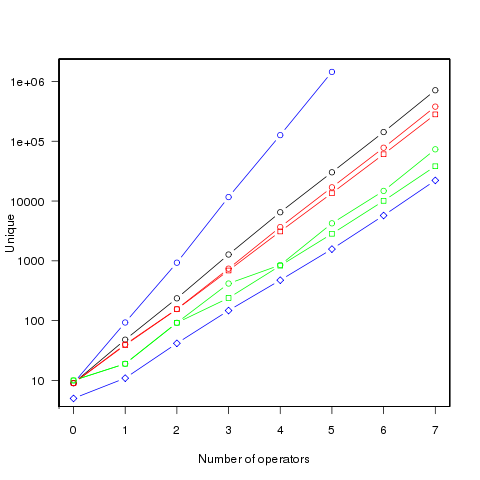
Limiting the operators to just add/multiply reduces the number of unique value possibilities. The difference increases linearly’ish to around 35% for seven operators.
The following uses colors to show the minimum number of operators needed to generate the given value, 1 is in the bottom left, 100,000 in the top right; red for one operator, yellow for two, green for three and so on.
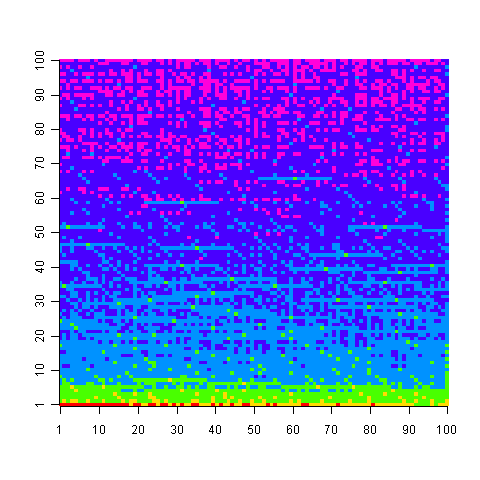
Knowing that N can be calculated using p operators does not mean that N-1 can also be generated using p operators; it is possible to generate 729 using two operators (i.e., 9*9*9), three operators are required to generate 92 and four to generate 417.
Values under the green line (first figure) are known to have solutions in the given number of operators; quickly obtaining the solution is another matter. There is at least a 50/50 chance that a randomly generated expression containing the given number of operators, and producing an integer value, will calculate a value on or below the diamond blue line. The overhead of storing precomputed minimal operator expressions is not that great for small numbers of operators.
Suggestions for a fast/low storage algorithm (random generation + modification through a cost function performs quite well) for large integer values welcome.
Update. Values from the first figure have been accepted by the On-Line Encyclopedia of Integer Sequences as entries: A181898, A181957, A181958, A181959 and A181960.
Recent Comments