Archive
2015 in the programming language standard’s world
Last Tuesday I was at the British Standards Institute for a meeting of IST/5, the programming languages committee.
My suggestion that the Cobol 2014 standard may be the last revision of that language appears to be coming true; there has been a steep decline in membership of the US Cobol committee (this is where all the work is done, with the rest of the world joining this committee or rubber stamping what comes out of it), and nobody has expressed interest in being involved in new work items.
Fortran appears to be going strong, with a revised standard planned for 2017.
In October C++ are rectifying the fact that they have not meet in Hawaii for three years. In fairness I ought to point out that the Fortran committee, when hosted by INCITS/PL22.3, regularly hold meetings in Las Vegas (I’m told its because the hotel rooms are cheap; Nevada is where US underground atom bomb tests were located and lots of super-computers executing programs written in Fortran were involved, or perhaps readers can think of an alternative explanation that does not invoke secret government organizations).
I found out that PL/1 is still an ISO Standard.
Work on the C and Ada standards continues.
Prolog has a new convenor, Ulrich Neumerkel. There was a meeting during April in Dresden, Germany but no minutes have been published. Did anybody attend?
ISO/IEC 23360-1:2006, the ISO version of the Linux Base Standard is almost 10 years behind the specification published by the organization who actually does the work. Some voices have expressed an interest in updating the ISO document. What does ISO’s version of the Linux Standard Base have to do with the committee responsible for programming languages?
Well, a long time ago in a galaxy far away, or the late 1980s in London, some people decided to set up a committee that specified O/S related library functions callable from C programs. SC22, programming languages, was the existing ISO committee having the closest fit with this new working group; initially it produced a specification that went under the name POSIX. Jump forward 15 years and Linux was the big POSIX success story (ok, the Linux people might see things differently) and dare I suggest that one of the motivations for creating ISO/IEC 23360-1:2006 might have been to bask in the reflected success of Linux. I understand the motivation of people involved in the standard’s process for wanting to published an update that reflects the current state of play (seriously out of date standards degrade the brand), but I don’t see why the Linux Foundation would be interested in going through the hassle of making this happen (unless they are having a mid-life crisis and are seeking approval of their work from an authority figure). Watch this blog for a 2016 status update.
Number of possible different one line programs
Writing one line programs is a popular activity in some programming languages (e.g., awk and Perl). How many different one line programs is it possible to write?
First we need to get some idea of the maximum number of characters that written on one line. Microsoft Windows XP or later has a maximum command line length of 8191 characters, while Windows 2000 and Windows NT 4.0 have a 2047 limit. POSIX requires that _POSIX2_LINE_MAX have a value of at least 2048.
In 2048 characters it is possible to assign values to and use at least once 100 different variables (e.g., a1=2;a2=2.3;....; print a1+a2*a3...). To get a lower bound lets consider the number of different expressions it is possible to write. How many functionally different expressions containing 100 binary operators are there?
If a language has, say, eight binary operators (e.g., +, -, *, /, %, &, |, ^), then it is possible to write 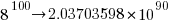 visually different expressions containing 100 binary operators. Some of these expressions will be mathematically equivalent (adopting the convention of leaving out the operands), e.g.,
visually different expressions containing 100 binary operators. Some of these expressions will be mathematically equivalent (adopting the convention of leaving out the operands), e.g., + * can also be written as * + (the appropriate operands will also have the be switched around).
If we just consider expressions created using the commutative operators (i.e., +, *, &, |, ^), then with these five operators it is possible to write 1170671511684728695563295535920396 mathematically different expressions containing 100 operators (assuming the common case that the five operators have different precedence levels, which means the different expressions have a one to one mapping to a rooted tree of height five); this 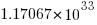 is a lot smaller than
is a lot smaller than 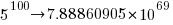 .
.
Had the approximately 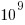 computers/smart phones in the world generated expressions at the rate of
computers/smart phones in the world generated expressions at the rate of 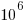 per second since the start of the Universe,
per second since the start of the Universe, 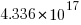 seconds ago, then the
seconds ago, then the 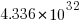 created so far would be almost half of the total possible.
created so far would be almost half of the total possible.
Once we start including the non-commutative operators such a minus and divide the number of possible combinations really starts to climb and the calculation of the totals is real complicated. Since the Universe is not yet half way through the commutative operators I will leave working this total out for another day.
Update (later in the day)
To get some idea of the huge jump in number of functionally different expressions that occurs when operator ordering is significant, with just the three operators -, / and % is is possible to create 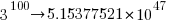 mathematically different expressions. This is a factor of
mathematically different expressions. This is a factor of 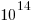 greater than generated by the five operators considered above.
greater than generated by the five operators considered above.
If we consider expressions containing just one instance of the five commutative operators then the number of expressions jumps by another two orders of magnitude to 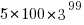 . This count will continue to increase for a while as more commutative operators are added and then start to decline; I have not yet worked things through to find the maxima.
. This count will continue to increase for a while as more commutative operators are added and then start to decline; I have not yet worked things through to find the maxima.
Update (April 2012).
Sequence A140606 in the On-Line Encyclopedia of Integer Sequences lists the number of inequivalent expressions involving n operands; whose first few values are: 1, 6, 68, 1170, 27142, 793002, 27914126, 1150212810, 54326011414, 2894532443154, 171800282010062, 11243812043430330, 804596872359480358, 62506696942427106498, 5239819196582605428254, 471480120474696200252970, 45328694990444455796547766, 4637556923393331549190920306
Recent Comments