Archive
Optimal function length: an analysis of the cited data
Careful analysis is required to extract reliable conclusions from data. Sloppy analysis can lead to incorrect conclusions being drawn.
The U-shaped plots cited as evidence for an ‘optimal’ number of LOC in a function/method that minimises the number of reported faults in a function, were shown to be caused by a mathematical artifact. What patterns of behavior are present in the data cited as evidence for an optimal number of LOC?
The 2000 paper Module Size Distribution and Defect Density by Malaiya and Denton summarises the data-oriented papers cited as sources on the issue of optimal length of a function/method, in LOC.
Note that the named unit of measurement in these papers is a module. In one paper, a module is specified as being as Ada package, but these papers specify that a module is a single function, method or anything else.
In order of publication year, the papers are:
The 1984 paper Software errors and complexity: an empirical investigation by Basili, and Perricone analyses measurements from a 90K Fortran program. The relevant Faults/LOC data is contained in two tables (VII and IX). Modules are sorted in to one of five bins, based on LOC, and average number of errors per thousand line of code calculated (over all modules, and just those containing at least one error); see table below:
Module Errors/1k lines Errors/1k lines
max LOC all modules error modules
50 16.0 65.0
100 12.6 33.3
150 12.4 24.6
200 7.6 13.4
>200 6.4 9.7 |
One of the paper’s conclusions: “One surprising result was that module size did not account for error proneness. In fact, it was quite the contrary–the larger the module, the less error prone it was.”
The 1985 paper Identifying error-prone software—an empirical study by Shen, Yu, Thebaut, and Paulsen analyses defect data from three products (written in Pascal, PL/S, and Assembly; there were three versions of the PL/S product) were analysed using Halstead/McCabe, plus defect density, in an attempt to identify error-prone software.
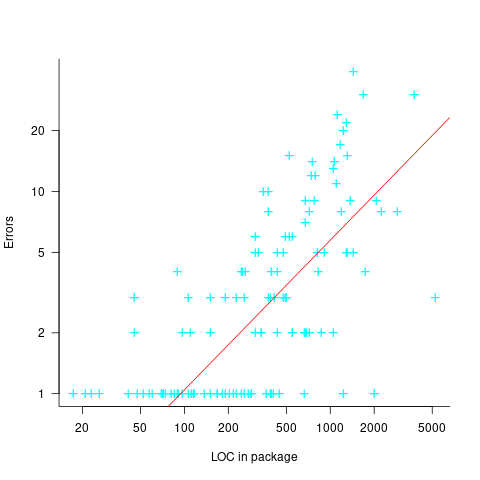
The paper includes a plot (figure 4) of defect density against LOC for one of the PL/S product releases, for 108 modules out of 253 (presumably 145 modules had no reported faults). The plot below shows defects against LOC, the original did not include axis values, and the red line is the fitted regression model 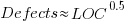 (data extracted using WebPlotDigitizer; code+data):
(data extracted using WebPlotDigitizer; code+data):
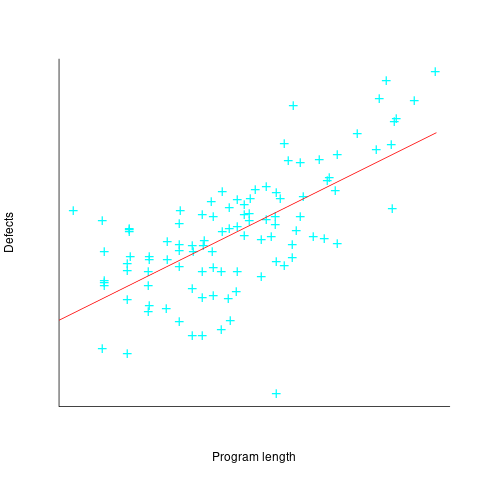
The power-law exponent is less than one, which suggests that defects per line is decreasing as module size increases, i.e., there is no optimal minimum, larger is always better. However, the analysis is incomplete because it does not include modules with zero reported defects.
The authors say: “… that there is a higher mean error rate in smaller sized modules, is consistent with that discovered by Basili and Perricone.”
The 1990 paper Error Density and Size in Ada Software by Carol Withrow analyses error data from a 114 KLOC military communication system written in Ada; of the 362 Ada packages, 137 had at least one error. The unit of measurement is an Ada package, which like a C++ class, can contain multiple definitions of types, variables, and functions.
The paper plots errors per thousand line of code against LOC, for packages containing at least one error, i.e., 62% of packages are not included in the analysis. The 137 packages are sorted into 8-bins, based on the number of lines they contain. The 52 packages in the 159-251 LOC bin have an average of 1.8 errors per 1 KLOC, which is the lowest bin average. The author concludes: “Our study of a large Ada project shows this optimal size to be about 225 lines.”
The plot below shows errors against LOC, red line is the fitted regression model 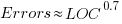 for
for 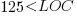 (data extracted using WebPlotDigitizer from figure 2; code+data):
(data extracted using WebPlotDigitizer from figure 2; code+data):
The 1993 paper An Empirical Investigation of Software Fault Distribution by Moller, and Paulish analysed four versions of a 750K product for controlling computer system utilization, written in assembler; the items measured were: DLOC (‘delta’ lines of code, DLOC, defined as “… the number of added or modified source lines of code for a version as compared to the prior version.”) and fault rate (faults per DLOC).
This paper is the first to point out that the code from multiple modules may need to be modified to fix a defect/fault/error. The following table shows the percentage of faults whose correction required changes to a given number of modules, for three releases of the product.
Modules
Version 1 2 3 4 5 6
a 78% 14% 3.4% 1.3% 0.2% 0.1%
b 77% 18% 3.3% 1.1% 0.3% 0.4%
c 85% 12% 2.0% 0.7% 0.0% 0.0% |
Modules are binned by DLOC and various plots appear in the paper; it’s all rather convoluted. The paper summary says: “With modified code, the fault rates steadily decrease as the module size increases.”
What conclusions does the Malaiya and Denton paper draw from these papers?
They present “… a model giving influence of module size on defect density based on data that has been reported. It provides an interpretation for both declining defect density for smaller modules and gradually rising defect density for larger modules. … If small modules can be
combined into optimal sized modules without reducing cohesion significantly, than the inherent defect density may be significantly reduced.”
The conclusion I draw from these papers is that a sloppy analysis in one paper obtained a result that sounded interesting enough to get published. All the other papers find defect/error/fault rate decreasing with module size (whatever a module might be).
Unique values generated by expressions of a given complexity
The majority of integer constants appearing in source code can be represented using a few bits. CPU designers use this characteristic when designing instruction sets, creating so called short-form or quick instructions that perform some operation involving small integer values, e.g., adding a value between 1 and 8 to a register. Writers of code optimizers are always looking for sequences of short-form instructions that are faster/smaller than the longer forms (the INMOS Transputer only had a short form for load immediate).
I have recently been looking at optimizing expressions written for a virtual machine that only supports immediate loads of decimal values between 1 an 9, and binary add/subtract/multiply/divide, e.g., optimizing an expression containing four operators, ((2*7)+9)*4+9 which evaluates to 101, to one containing three operators, (8+9)*6-1 also evaluates to 101. Intermediate results can have fractional values, but I am only interested in expressions whose final result has an integer value (i.e., zero fractional part).
A little thought shows that the value of an expression containing a subexpression whose value includes a fractional value (e.g., 1/3) can always be generated by an expression containing the same or a fewer number of operators and no intermediate fractional value intermediate results (e.g., 9/(1/5) can be generated using 9*5, i.e., the result of any divide operation always has to be an integer if the final result is to be a unique integer. Enumerating the unique set of values generated by expressions containing a given number of operators shows that divide is redundant for expressions containing six of fewer operators and only adds 11 unique values for seven operators (379,073 possibilities without divide)
Removing support for the minus operator only reduces the size of the result set by around 10%. Possibly being worthwhile time saving for expressions containing many operators or searching for an expression whose result value is very large.
There does not appear to be a straightforward (and fast) algorithm that returns the minimal operation expression for a given constant.
I wrote an R program to exhaustively generate all integer values returned by expressions containing up to seven operators. To find out how many different values, integer/real, could be calculated I wrote a maxima program (this represents fractional values using a rational number representation and exceeds 4G byte of storage for expressions containing more than five operators).
The following figure shows the number of different values that can be generated by an expression containing a given number of operators (blue), the number of integer values (black), the number of positive integer values (red), the smallest positive integer that cannot be calculated by an expression containing the given number of operators (green) (circles are for add/subtract/multiply/divide, squares for add/multiply). Any value below a green line is guaranteed to have a solution in the in the given number of operators (or fewer). The blue diamond line is the mean value of a random expression containing the given number of operators.
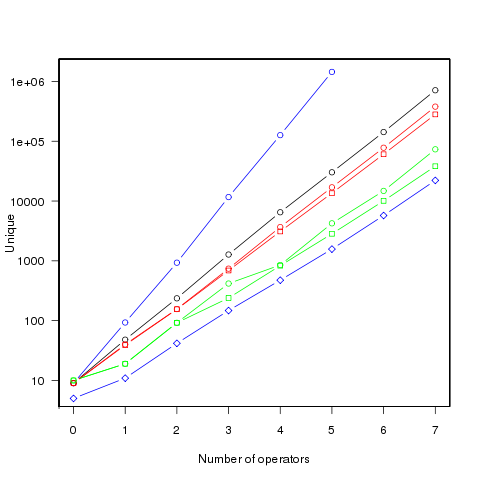
Limiting the operators to just add/multiply reduces the number of unique value possibilities. The difference increases linearly’ish to around 35% for seven operators.
The following uses colors to show the minimum number of operators needed to generate the given value, 1 is in the bottom left, 100,000 in the top right; red for one operator, yellow for two, green for three and so on.
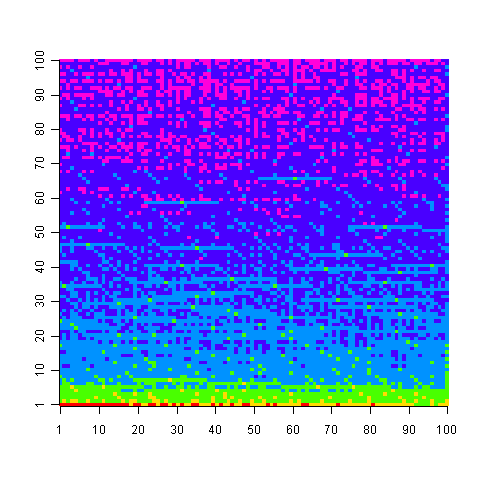
Knowing that N can be calculated using p operators does not mean that N-1 can also be generated using p operators; it is possible to generate 729 using two operators (i.e., 9*9*9), three operators are required to generate 92 and four to generate 417.
Values under the green line (first figure) are known to have solutions in the given number of operators; quickly obtaining the solution is another matter. There is at least a 50/50 chance that a randomly generated expression containing the given number of operators, and producing an integer value, will calculate a value on or below the diamond blue line. The overhead of storing precomputed minimal operator expressions is not that great for small numbers of operators.
Suggestions for a fast/low storage algorithm (random generation + modification through a cost function performs quite well) for large integer values welcome.
Update. Values from the first figure have been accepted by the On-Line Encyclopedia of Integer Sequences as entries: A181898, A181957, A181958, A181959 and A181960.
Compiling to reduce the impact of soft errors on program output
Optimizing compilers have traditionally made code faster and smaller (sometimes a choice has to be made between faster/larger and slower/smaller). The huge growth in the use of battery power devices has created a new attribute for writers of optimizers to target, finding code sequences that minimise power consumption (I previously listed this as a major growth area in the next decade). Radiation (e.g., from cosmic rays) can cause a memory or processor bit to flip, known as a soft error, and I have recently been reading about how code can be optimized to reduce the probability that soft errors will alter the external behavior of a running program.
The soft error rate is usually quoted in FITs (Failure in Time), with 1 FIT corresponding to 1 error per 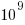 hours per megabit, or
hours per megabit, or 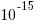 errors per bit-hour. A PC with 4 GB of DRAM (say 1000 FIT/Mb which increases with altitude and is 10 times greater in Denver Colorado) has a MTBF (mean time between failure) of
errors per bit-hour. A PC with 4 GB of DRAM (say 1000 FIT/Mb which increases with altitude and is 10 times greater in Denver Colorado) has a MTBF (mean time between failure) of 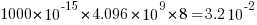 hours, around once every 33 hours. Calculating the FIT for processors is complicated.
hours, around once every 33 hours. Calculating the FIT for processors is complicated.
Uncorrected soft errors place a limit on the maximum number of computing nodes that can be usefully used by one application. At around 50,000 nodes a system will be spending half its time saving checkpoints and restarting from previous checkpoints after an error occurs.
Why not rely on error correcting memory? Super computers containing terrabytes are built containing error correcting memory, but this does not make the problem go away, it ‘only’ reduces it by around two orders of magnitude. Builders of commodity processors don’t use much error correction circuitry because it would increase costs/power consumption/etc for an increased level of reliability that the commodity market is not interested in; vendors of high-end processors add significant amounts of error correction circuitry.
Most of the compiler research I am aware of involves soft errors occurring on the processor and this topic is discussed below; there has been some work on assigning variables deemed to be critical to a subset of memory that is protected with error correcting hardware. Pointers to other compiler research involving memory soft errors welcome.
A commonly used technique for handling hardware faults is redundancy, usually redundant hardware (e.g., three processors performing the same calculating and a majority vote used to decide which of the outputs to accept). Software only approaches include the compiler generating two or more independent machine code sequences for each source code sequence whose computed values are compared at various check points and running multiple copies of a program in different threads and comparing outputs. The
Shoestring compiler (based on llvm) takes a lightweight approach to redundancy by not duplicating those code sequences that are less affected by register bit flips (e.g., the value obtained from a bitwise AND that extracts 8 bits from a 32-bit register is 75% less likely to deliver an incorrect result than an operation that depends on all 32 bits).
The reliability of single ‘thread’ generated code can be improved by optimizing register lifetimes for this purpose. A value is loaded into a register and sometime later it is used one or more times. A soft error corrupting register contents after the last use of the value it contains has no impact on program execution, the soft error has to occur between the load and last use of the value for it to possibly influence program output. One group of researchers modified a compiler (Trimaran) to order register usage such that the average interval between load and last usage was reduced by 10%, compared to the default behavior.
Developers don’t have to wait for compiler or hardware support, they can improve reliability by using algorithms that are robust in the presence of ‘faulty’ hardware. For instance, the traditional algorithms for two-process mutual exclusion are not fault tolerant; a fault tolerant mutual exclusion algorithm using 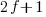 variables, where a single fault may occur in up to
variables, where a single fault may occur in up to 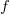 variables is available.
variables is available.
Searching for the source line implementing 3n+1
I have been doing some research on the variety of ways that different developers write code to implement the same specification and have been lucky enough to obtain the source code of approximately 6,000 implementations of a problem based on the 3n+1 algorithm. At some point this algorithm requires multiplying a value by three and adding one, e.g., n=3*n+1;.
While I expected some variation in the coding of many parts of the algorithm I did not expect to see much variation in the n=n*3+1;. I was in for a surprise, the following are some of the different implementations I have seen so far:
n = n + n + n + 1 ;
n += n + n + 1;
n = (n << 1) + n + 1;
n += (n << 1) + 1;
n *= 3; n++;
t = (n << 1) ; n = t + n + 1;
n = (n << 2) - n + 1;
I was already manually annotating the source and it was easy for me to locate the line implementing
I mentioned this search problem over drinks after a talk I gave at the Oxford branch of the ACCU last week and somebody (Huw ???) suggested that perhaps the code generated by gcc would be the same no matter how 3n+1 was implemented. I could see lots of reasons why this would not be the case, but the idea was interesting and worth investigation.
At the default optimization level the generated x86 code is different for different implemenetations, but optimizing at the “-O 3” level results in all but one of the above expressions generating the same evaluation code:
leal 1(%rax,%rax,2), %eax |
The exception is (n << 2) - n + 1 which results in shift/subtract/add. Perhaps I should report this as a bug in gcc :-)
I was surprised that gcc exhibited this characteristic and I plan to carry out more tests to trace out the envelope of this apparent "same generated code for equivalent expressions" behavior of gcc.
Recent Comments