Archive
Optimizing floating-point expressions for accuracy
Floating-point arithmetic is one topic that most compiler writers tend to avoid as much as possible. The majority of programs don’t use floating-point (i.e., low customer demand), much of the analysis depends on the range of values being operated on (i.e., information not usually available to the compiler) and a lot of developers don’t understand numerical methods (i.e., keep the compiler out of the blame firing line by generating code that looks like what appears in the source).
There is a scientific and engineering community whose software contains lots of floating-point arithmetic, the so called number-crunchers. While this community is relatively small, many of the problems it works on attract lots of funding and some of this money filters down to compiler development. However, the fancy optimizations that appear in these Fortran compilers (until the second edition of the C standard in 1999 Fortran did a much better job of handling the minutia of floating-point arithmetic) are mostly about figuring out how to distribute the execution of loops over multiple functional units (i.e., concurrent execution).
The elephant in the floating-point evaluation room is result accuracy. Compiler writers know they have to be careful not to throw away accuracy (e.g., optimizing out what appear to be redundant operations in the Kahan summation algorithm), but until recently nobody had any idea how to go about improving the accuracy of what had been written. In retrospect one accuracy improvement algorithm is obvious, try lots of possible combinations of the ways in which an expression can be written and pick the most accurate.
There are lots of ways in which the operands in an expression can be paired together to be operated on; some of the ways of pairing the operands in a+b+c+d include (a+b)+(c+d), a+(b+(c+d)) and (d+a)+(b+c) (unless the source explicitly includes parenthesis compilers for C, C++, Fortran and many other languages (not Java which is strictly left to right) are permitted to choose the pairing and order of evaluation). For n operands (assuming the operators have the same precedence and are commutative) the number is combinations is 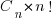 where
where 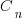 is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands
is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands 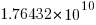 of which
of which 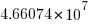 are unique.
are unique.
A recent study by Langlois, Martel and Thévenoux analysed the accuracy achieved by all unique permutations of ten operands on four different data sets. People within the same umbrella project are now working on integrating this kind of analysis into a compiler. This work is another example of the growing trend in compiler research of using the processing power provided by multiple cores to use algorithms that were previously unrealistic.
Over the last six years or so there has been lot of very interesting floating-point work going on in France, with gcc and llvm making use of the MPFR library (multiple-precision floating-point) for quite a while. Something very new and interesting is RangeLab which, given the lower/upper bounds of each input variable to a program (a simple C-like language) computes the range of the outputs as well as ranges for the roundoff errors (the tool assumes IEEE floating-point arithmetic). I now know that over the range [800, 1000] the expression x*(x+1) is a lot more accurate than x*x+x.
Update: See comment from @Eric and my response below.
Recent Comments