Archive
Comparing expression usage in mathematics and C source
Why does a particular expression appear in source code?
One reason is that the expression is the coded form of a formula from the application domain, e.g., 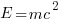 .
.
Another reason is that the expression calculates an algorithm/housekeeping related address, or offset, to where a value of interest is held.
Most people (including me, many years ago) think that the majority of source code expressions relate to the application domain, in one-way or another.
Work on a compiler related optimizer, and you will soon learn the truth; most expressions are simple and calculate addresses/offsets. Optimizing compilers would not have much to do, if they only relied on expressions from the application domain (my numbers tool throws something up every now and again).
What are the characteristics of application domain expression?
I like to think of them as being complicated, but that’s because it used to be in my interest for them to be complicated (I used to work on optimizers, which have the potential to make big savings if things are complicated).
Measurements of expressions in scientific papers is needed, but who is going to be interested in measuring the characteristics of mathematical expressions appearing in papers? I’m interested, but not enough to do the work. Then, a few weeks ago I discovered: An Analysis of Mathematical Expressions Used in Practice, by Clare So; an analysis of 20,000 mathematical papers submitted to arXiv between 2000 and 2004.
The following discussion uses the measurements made for my C book, as the representative source code (I keep suggesting that detailed measurements of other languages is needed, but nobody has jumped in and made them, yet).
The table below shows percentage occurrence of operators in expressions. Minus is much more common than plus in mathematical expressions, the opposite of C source; the ‘popularity’ of the relational operators is also reversed.
Operator Mathematics C source = 0.39 3.08 - 0.35 0.19 + 0.24 0.38 <= 0.06 0.04 > 0.041 0.11 < 0.037 0.22 |
The most common single binary operator expression in mathematics is n-1 (the data counts expressions using different variable names as different expressions; yes, n is the most popular variable name, and adding up other uses does not change relative frequency by much). In C source var+int_constant is around twice as common as var-int_constant
The plot below shows the percentage of expressions containing a given number of operators (I’ve made a big assumption about exactly what Clare So is counting; code+data). The operator count starts at two because that is where the count starts for the mathematics data. In C source, around 99% of expressions have less than two operators, so the simple case completely dominates.
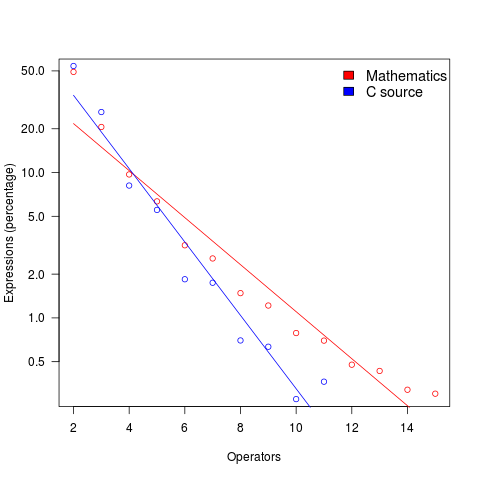
For expressions containing between two and five operators, frequency of occurrence is sort of about the same in mathematics and C, with C frequency decreasing more rapidly. The data disagrees with me again…
Mathematical proofs contain faults, just like software
The idea of proving programs correct, like mathematical proofs, is appealing, but is based on an incorrect assumption often made by non-mathematicians, e.g., mathematical proofs are fault free. In practice, mathematicians make mistakes and create proofs that contain serious errors; those of us who are taught mathematical techniques, but are not mathematicians, only get to see the good stuff that has been checked over many years.
An appreciation that published proofs contain mistakes is starting to grow, but Magnificent mistakes in mathematics is an odd choice for a book title on the topic. Quotes from De Millo’s article on “Social Processes and Proofs of Theorems and Programs” now appear regularly; On proof and progress in mathematics is worth a read.
Are there patterns to the faults that appear in claimed mathematical proofs?
- The difficulty of the problem is one obvious issue, as shown by the faulty proofs of the N vs. NP problem,
- the size of the proof, in number of pages, is a common problem, with Mochizuki’s ‘proof’ of the ABC conjecture being a recent example and the Hales-Ferguson proof of the Kepler conjecture has a whole book dedicated to trying to figure out if the proof is correct,
- number of people involved: some of the 100+ mathematicians responsible for proving components of the classification of finite simple groups died before the proof was claimed to be complete; the proofs of the various components created the largest known claimed proof, at tens of thousands of pages.
A surprisingly common approach, used by mathematicians to avoid faults in their proofs, is to state theorems without giving a formal proof (giving an informal one is given instead). There are plenty of mathematicians who don’t think proofs are a big part of mathematics (various papers from the linked-to book are available as pdfs).
Next time you encounter an advocate of proving programs correct using mathematics, ask them what they think about the uncertainty about claimed mathematical proofs and all the mistakes that have been found in published proofs.
What is the error rate for published mathematical proofs?
Mathematical proofs are sometimes cited as the gold standard against which software quality should be compared. At school we rarely get to hear about proofs that turn out to be wrong and are inculcated with the prevailing wisdom that all mathematical proofs are correct.
There are many technical and social issues involved in believing a published proof and well known established mathematicians have no trouble pointing out that “… it is impossible to write out a very long and complicated argument without error, …”
Examples of incorrect published proofs include Wiles’ first proof of Fermat’s Last Theorem and an serious error found in a proof of a message signing scheme.
A question on mathoverflow contains a list of rather interesting false proofs.
Then, of course, there are always those papers that appear in journals that get written about more frequently on Retraction Watch than others.
What is the error rate for published mathematical proofs? I have not been able to find any collection of mathematical proof error data.
Several authors have expressed the view that because there so many diverse mathematical topics being studied these days there are very few domain experts available to check proofs. A complicated proof of a not particularly interesting result is unlikely to attract the attention needed to check it thoroughly. It should come as no surprise that the number of known errors in such proofs is equal to the number of known errors in programs that have never been executed.
Proofs are different from programs in that one error can be enough to ‘kill-off’ a proof, while a program can contain many errors and still be useful. Do errors in programs get talked about more than errors in proofs? I rarely get to socialize with working mathematicians and so cannot make any judgment call on this question.
Every non-trivial program is likely to contain many errors; can the same be said for long mathematical proofs? Are many of these errors as trivial (in the sense that they are easily fixed) as errors in programs?
One commonly used error rate for programs is errors per line of code; how should the rate be expressed for proofs? Errors per page, per line, per definition?
Lots of questions and I’m hoping one of my well informed readers will be able to provide some answers or at least cite a reference that does.
Abramowitz and Stegun mark II
Like me I imagine many readers have owned a copy of Handbook of Mathematical Functions (or to use its more well known name “Abramowitz and Stegun”, after its two editors). Some time ago I heard that an updated handbook was being created, time passed and last year the “NIST Handbook of Mathematical Functions” was published, the companion web site has been slowing evolving over the years.
I did not hear anybody raving about the updated handbook and it was priced at more than twice that of the original (whose copyright was in the public domain and thus open to Dover to print a low cost edition {and others to make available online}, NIST are claiming copyright over the updated version which is published by Cambridge University press), so did not rush out to buy a copy.
I recently placed a large order with Amazon US and was tempted by a temporary price reduction to buy the NIST handbook (tip for Europeans: it is often possible to make big savings by ordering from amazon.com, which seems to ship from Germany and arrives a few days later than orders placed with amazon.co.uk),
Summary recommendation:
- Should somebody who has the original handbook buy the update? Probably not.
- If somebody had a choice of either, which should they pick? I would go for the original handbook.
The major difference between the handbooks are that the substantial number of precomputed tables of values of functions are not included in the update and there are 12 new chapters covering subjects not included (or not given much prominence) in the original. A not so important difference is the switch from black&white to color in the update, this works well in the online version (on the CD shipped with the book) but works poorly in print form; if a book is intended to be printed its color usage needs to be optimized for reflected light which has different characteristics than the transmitted light of a display..
The argument for removing the tables of values is that software packages can now be used to obtain these. In practice I rarely use the tables of values for this purpose; I use the tables to find the range of function input values that will generate a given rang of output values, or to see how output values change with changes in input values. For me omitting these tables in the update was a big mistake; ok the number of significant digits could have been reduced (to say five) to save some paper. The new chapters often contain various tables of numbers, but they are not extensive, but a conscious decisions seems to have been made to remove tables from existing chapters.
From a user interface point of view I don’t like the glossy paper used in the update, presumably caused by the switch to color which does not work well in the printed version; the angle of the page has to be constantly shifted to reduce glare from overhead lights and the handbook is noticeably heavier even though the page count is down by around 20% (886 vs 1030, excluding index which is substantially improved in the update).
The original has lots of tables, matte pages that don’t glare and is surprisingly light for such a big book. Time will tell whether I find the new chapters useful.
Proving software correct
Users want confidence that software is ‘correct’; what constitutes correct depends on who you talk to and can vary between doing what the user expects and behaving according to a specification (which may include behavior that users did not expect or want).
The gold standard for software correctness is that achieved by mathematical proofs, or at least what most people believe is achieved by such proofs, i.e., a statement that is shown through a sequence of steps to be derived from a set of axioms. The sequence of steps used in most real proofs operate at a much higher level than axioms and rely on the reader to fill in the gaps left between each step. Ever since theorems were first stated they sometimes contained faults, i.e., were not correct theorems, and as mathematicians have continued to increase the size and complexity of theorems being ‘proved’ the technical and social issues involved in believing a published proof have grown in complexity.
Software proofs usually operate by translating the source in to some mathematical formalism and using a theorem prover to show that one or more properties are met. Perhaps the most famous use of such a proof that had an outcome different than that predicted is the 1996 Ariane 5 rocket crash; various proofs had been obtained for the Ariane 4 software showing that the value of some variables would never exceed given limits, these proofs involved input values that depended on the performance of the rocket and because Ariane 5 was more powerful than Ariane 4 the proofs were no longer valid (management would have found this out had they recheck the proofs using the larger values). Update: My only knowledge of this work comes from a conversation I recall with somebody working in the formal verification area, I no longer have contact with them and the company they worked for no longer exists; Pascal Cuoq’s comment below suggests they may have overstated the formal nature of the work, I have no means of double checking.
Purveyors of ‘software proof’ systems will tell you about the importance of feeding in the correct input values and will tell you about the known proofs they have managed to verify using their system. The elephant in the room that rarely gets mentioned is the correctness of the program that translates source code into the mathematical formalism used. These translators often handle that subset of the language which is relatively easy to map to the target formalism, the MALPAS C to IL translator is one exception to this (ok, yes my company wrote this translator so the opinion might be a little biased).
The method commonly associated with claims of correctness proof for a translator or compiler is slightly different from that described above for applications. This method involves manually writing some mathematics, using the chosen formalism, that ‘implements’ the translator/compiler. Strangely there are people who think that doing this is sufficient to claim the compiler is ‘verified’ or ‘proved correct’. As any schoolboy knows it is possible to write mathematics that contains mistakes and the writing of a mathematical implementation is just the first step in a process intended to increase confidence in a claim of correctness.
One of the questions that might be asked of a ‘mathematics implementation’ of a compiler is: does it faithfully interpret source code syntax/semantics according to the syntax/semantics specified in the appropriate language document?
Answering this question requires that the language syntax/semantics be specified in some mathematical notation that is amenable to formal analysis. Various researchers have created mathematical models for languages such as Ada, CHILL and C. However, these models are not recognized as being definitive, that status belongs to the corresponding ISO Standard written in English prose. The Modula-2 standard is specified using both English prose and equivalent mathematical notation with both having equal status as the definition of the language (any inconsistency between the two is decided why analyzing what behavior was intended); there were lots of plans to do stuff with this mathematics but the ISO language committee struggled just to produce a tool capable of printing the mathematics.
The developers of the Compcert system refer to it as a formally verified C compiler front-end when the language actually verified is called Clight, which they describe as a subset of the C language. This is very interesting work and I hope they continue to refine it and add support for more C-like constructs. But let’s be clear, the one thing missing from this project is any proof of a connection to the requirements contained in the C Standard.
I don’t know what it is about formal verification but those involved can at the same time be both very particular about the language they use in their mathematics and completely over the top in the claims they make about what their tools do. A speaker from Polyspace at one MISRA C conference claimed his tool could detect 100% of the coding guidelines specified in MISRA C, a surprising achievement for a runtime tool (as it was then) enforcing requirements mainly aimed at source code; I eventually got him to agree that the tool detected 100% of the constructs specified by the small subset of guidelines they had implemented.
I doubt that the Advertising Standard Authority would allow adverts containing the claims made by some formal verification advocates to appear in print or on TV; if soap manufacturers have to follow ASA rules then so should formal verification researchers.
Without a language specification written in a form amenable to mathematical analysis any claims of correctness have to be based on the traditional means of reading English prose very carefully and writing lots of tests to probe every obscure corner of the language specification. This was the approach used for the production of the Model Implementation of C, a system designed to detect all unspecified, implementation defined and undefined uses in C programs (it used a compiler, linker and interpreter). One measure of how well an implementor has studied the standard is how many faults they have discovered in it (some people claim this is a quality of standard issue, but the similar number of defects reported against the Ada and C Standards show that at least for Ada this is not true); here are some from the Model Implementation project.
Performance on independently written tests can be a good indicator of implementation correctness, depending on the quality of the tests. Both the Perennial and PlumHall C validation suites are of high quality, while suites such as the gcc testsuite are rather ad-hoc, have poor coverage and tend to be runtime oriented. The problem with high quality validation suites is that they cost enough money to put them out of reach of many research groups (I suspect another problem is that such groups don’t understand the benefits of using such suites or think they can do just as good a job in a few weeks).
Recently a new formal verification tool for C has appeared that performs all its verification checking at program runtime, i.e., after the user source has been translated to executable form. It is still very early days for kcc (they have yet to chose a name and the command used to invoke the translator is currently being used), they have an initial system up and running and are keen to continue improving it.
I am interested in the system because of what it might evolve into, including:
- a means of quickly checking the behavior of obscure bits of code (I get asked all sorts of weird questions and my brain is not always willing to switch to C language lawyer mode),
- a means of checking the consistency of the requirements in the C Standard, which will require another tool making use of the formalism built up by kcc,
- a tool which would help developers understand which parts of the C Standard they need to look at to understand some construct (the tool currently has a trace mode that needs lots of work).
The sound of code
Speech, it is claimed, is the ability that separates humans from all other animals, yet working with code is almost exclusively based on sight. There are instances of ‘accidental’ uses of sound, e.g., listening to disc activity to monitor a programs process or in days of old the chatter of other mechanical parts.
Various projects have attempted to intentionally make use of sound to provide an interface to the software development process, including:
People like to talk about what they do and perhaps this could be used to overcome developers dislike of writing comments. Unfortunately automated processing of natural language (assuming the speech to text problem is solved) has not reached the stage where it is possible to automatically detect when the topic of conversation has changed or to figure out what piece of code is being discussed. Perhaps the reason why developers find it so hard to write good comments is because it is a skill that requires training and effort, not random thoughts that happen to come to mind.
Rather than relying on the side-effects of mechanical vibration it has been proposed that programs intentionally produce audio output that aids developers monitor their progress. Your authors experience with interpreting mechanically generated sound is that it requires a great deal of understanding of a program’s behavior and that it is a very low bandwidth information channel.
Writing code by talking (i.e., voice input of source code) initially sounds attractive. As a form of input speech is faster than typing, however computer processing of speech is still painfully slow. Another problem that needs to be handled is the large number of different ways in which the same thing can and is spoken, e.g., numeric values. As a method of output reading is 70% faster than listening.
Unless developers have to spend lots of time commuting in person, rather than telecommuting, I don’ see a future for speech input of code. Audio program execution monitoring probably has market is specialist niches, no more.
I do see a future for spoken mathematics, which is something that people who are not a mathematicians might want to do. The necessary formating commands are sufficiently obtuse that they require too much effort from the casual user.