Archive
Unique values generated by expressions of a given complexity
The majority of integer constants appearing in source code can be represented using a few bits. CPU designers use this characteristic when designing instruction sets, creating so called short-form or quick instructions that perform some operation involving small integer values, e.g., adding a value between 1 and 8 to a register. Writers of code optimizers are always looking for sequences of short-form instructions that are faster/smaller than the longer forms (the INMOS Transputer only had a short form for load immediate).
I have recently been looking at optimizing expressions written for a virtual machine that only supports immediate loads of decimal values between 1 an 9, and binary add/subtract/multiply/divide, e.g., optimizing an expression containing four operators, ((2*7)+9)*4+9 which evaluates to 101, to one containing three operators, (8+9)*6-1 also evaluates to 101. Intermediate results can have fractional values, but I am only interested in expressions whose final result has an integer value (i.e., zero fractional part).
A little thought shows that the value of an expression containing a subexpression whose value includes a fractional value (e.g., 1/3) can always be generated by an expression containing the same or a fewer number of operators and no intermediate fractional value intermediate results (e.g., 9/(1/5) can be generated using 9*5, i.e., the result of any divide operation always has to be an integer if the final result is to be a unique integer. Enumerating the unique set of values generated by expressions containing a given number of operators shows that divide is redundant for expressions containing six of fewer operators and only adds 11 unique values for seven operators (379,073 possibilities without divide)
Removing support for the minus operator only reduces the size of the result set by around 10%. Possibly being worthwhile time saving for expressions containing many operators or searching for an expression whose result value is very large.
There does not appear to be a straightforward (and fast) algorithm that returns the minimal operation expression for a given constant.
I wrote an R program to exhaustively generate all integer values returned by expressions containing up to seven operators. To find out how many different values, integer/real, could be calculated I wrote a maxima program (this represents fractional values using a rational number representation and exceeds 4G byte of storage for expressions containing more than five operators).
The following figure shows the number of different values that can be generated by an expression containing a given number of operators (blue), the number of integer values (black), the number of positive integer values (red), the smallest positive integer that cannot be calculated by an expression containing the given number of operators (green) (circles are for add/subtract/multiply/divide, squares for add/multiply). Any value below a green line is guaranteed to have a solution in the in the given number of operators (or fewer). The blue diamond line is the mean value of a random expression containing the given number of operators.
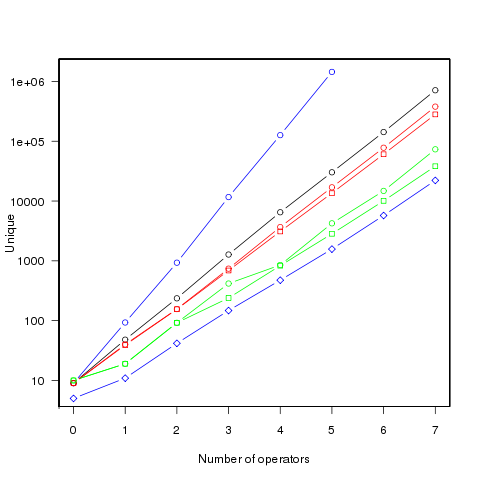
Limiting the operators to just add/multiply reduces the number of unique value possibilities. The difference increases linearly’ish to around 35% for seven operators.
The following uses colors to show the minimum number of operators needed to generate the given value, 1 is in the bottom left, 100,000 in the top right; red for one operator, yellow for two, green for three and so on.
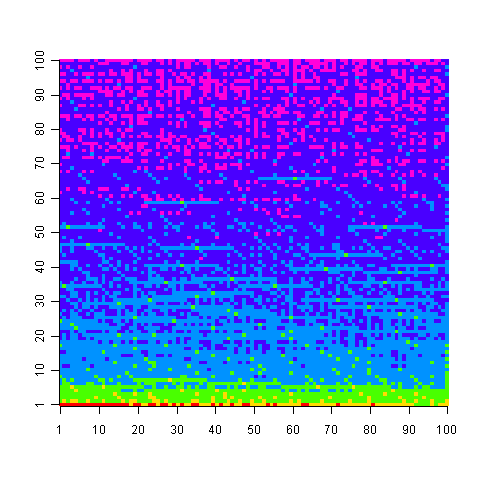
Knowing that N can be calculated using p operators does not mean that N-1 can also be generated using p operators; it is possible to generate 729 using two operators (i.e., 9*9*9), three operators are required to generate 92 and four to generate 417.
Values under the green line (first figure) are known to have solutions in the given number of operators; quickly obtaining the solution is another matter. There is at least a 50/50 chance that a randomly generated expression containing the given number of operators, and producing an integer value, will calculate a value on or below the diamond blue line. The overhead of storing precomputed minimal operator expressions is not that great for small numbers of operators.
Suggestions for a fast/low storage algorithm (random generation + modification through a cost function performs quite well) for large integer values welcome.
Update. Values from the first figure have been accepted by the On-Line Encyclopedia of Integer Sequences as entries: A181898, A181957, A181958, A181959 and A181960.
Optimizing floating-point expressions for accuracy
Floating-point arithmetic is one topic that most compiler writers tend to avoid as much as possible. The majority of programs don’t use floating-point (i.e., low customer demand), much of the analysis depends on the range of values being operated on (i.e., information not usually available to the compiler) and a lot of developers don’t understand numerical methods (i.e., keep the compiler out of the blame firing line by generating code that looks like what appears in the source).
There is a scientific and engineering community whose software contains lots of floating-point arithmetic, the so called number-crunchers. While this community is relatively small, many of the problems it works on attract lots of funding and some of this money filters down to compiler development. However, the fancy optimizations that appear in these Fortran compilers (until the second edition of the C standard in 1999 Fortran did a much better job of handling the minutia of floating-point arithmetic) are mostly about figuring out how to distribute the execution of loops over multiple functional units (i.e., concurrent execution).
The elephant in the floating-point evaluation room is result accuracy. Compiler writers know they have to be careful not to throw away accuracy (e.g., optimizing out what appear to be redundant operations in the Kahan summation algorithm), but until recently nobody had any idea how to go about improving the accuracy of what had been written. In retrospect one accuracy improvement algorithm is obvious, try lots of possible combinations of the ways in which an expression can be written and pick the most accurate.
There are lots of ways in which the operands in an expression can be paired together to be operated on; some of the ways of pairing the operands in a+b+c+d include (a+b)+(c+d), a+(b+(c+d)) and (d+a)+(b+c) (unless the source explicitly includes parenthesis compilers for C, C++, Fortran and many other languages (not Java which is strictly left to right) are permitted to choose the pairing and order of evaluation). For n operands (assuming the operators have the same precedence and are commutative) the number is combinations is 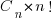 where
where 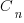 is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands
is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands 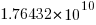 of which
of which 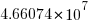 are unique.
are unique.
A recent study by Langlois, Martel and Thévenoux analysed the accuracy achieved by all unique permutations of ten operands on four different data sets. People within the same umbrella project are now working on integrating this kind of analysis into a compiler. This work is another example of the growing trend in compiler research of using the processing power provided by multiple cores to use algorithms that were previously unrealistic.
Over the last six years or so there has been lot of very interesting floating-point work going on in France, with gcc and llvm making use of the MPFR library (multiple-precision floating-point) for quite a while. Something very new and interesting is RangeLab which, given the lower/upper bounds of each input variable to a program (a simple C-like language) computes the range of the outputs as well as ranges for the roundoff errors (the tool assumes IEEE floating-point arithmetic). I now know that over the range [800, 1000] the expression x*(x+1) is a lot more accurate than x*x+x.
Update: See comment from @Eric and my response below.
Recent Comments