Archive
Maths GCE from 1972 (paper 2)
While sorting through some old papers I came across my GCE maths O level exam papers from the summer of 1972. They are known as GCSE exams these days and are taken by 16 year olds at the end of their final year of compulsory education in the UK. I was lucky enough to have a maths teacher who believed in encouraging students to excel and I (plus five others) took this exam when we were 15. I never got the chance to thank Mr Merritt for the profound effect he had on my life.
For many years the average grades achieved by students in the UK has had a steady upward trend and some people claim the exams are getting easier (others that students are better taught, or at least better taught to pass exams). These days students have calculators and don’t use log tables, so question 3 of Section A is not applicable.
Exam papers in the UK are written by various examining boards. Mine were from the University of London, Syllabus D. I have two papers labeled “Mathematics 2” and “Mathematics 3” and don’t recall if there was ever a “Mathematics 1”. The following are the questions from “Mathematics 2”.
All necessary working must be shown.
- Factorise
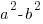
Hence, or otherwise, find the exact value of
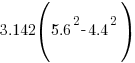
4 marks
- Given that
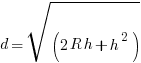 , express
, express 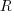 in terms of
in terms of 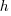 and
and 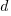 .
.
3 marks
- Use four digit tables to evaluate
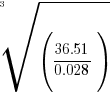 .
.
4 marks
- Given that
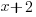 is a factor of
is a factor of 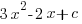 , calculate the value of
, calculate the value of 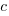 .
.
3 marks
-
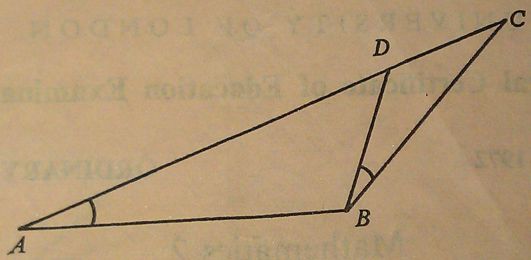
In the diagram ∠DBC = ∠BAD and ADC is a straight line. State which of the two triangles are similar.
If AB = 7 cm, BC = 6 cm and DC = 4 cm, calculate the lengths of AC and BD.
5 marks
- A bicycle wheel has diameter 35 cm. Calculate how many revolutions it makes every minute when the bicycle is travelling at 33 km/h. [ Take
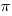 as 22/7 ]
as 22/7 ]
4 marks
- Calculate the gradient of the curve
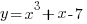 at the point (1, -5). Calculate also the coordinates of the point on the curve where the gradient is 1.
at the point (1, -5). Calculate also the coordinates of the point on the curve where the gradient is 1.
4 marks
-
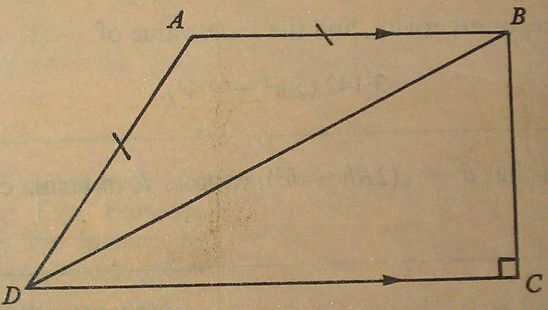
In the diagram, AB is parallel to DC, AB = AD and ∠C = 90°. Prove that ∠DAB = 2∠DBC.
5 marks
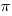 as 3.142 when required
as 3.142 when required- A ship is at the point P (54°N, 55°W). Calculate the distance, in nautical miles, of P from the equator.
The ship then sails 500 nautical miles due East to a point Q. Calculate the latitude and longitude of Q.
An aircraft flies due South at a constant height of 10 000 m from the point vertically above P to a point vertically above the equator. Taking the earth to be a sphere of radius 6 370 km, calculate the length of the arc along which the aircraft flies.
17 marks
- Draw a circle of radius 5.5 cm. Using ruler and compasses only, construct a tangent to the circle at any point A on its circumference.
Using a protractor, construct the points A, B and C on this circle so that the angles A, B and C of the triangle ABC are 50°, 56° and 74° respectively.
By a further construction using ruler and compasses only, obtain a point X on the tangent at A which is equidistant from the lines AB and BC.
Measure the length of AX.
17 marks
- (i) Find the smallest positive term in the arithmetic progression 76, 74½, 73 … .
Find also the number of positive terns in the progression and the sum of these positive terms.
(ii) The first and fourth terms in a geometric progression are
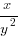 and
and 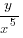 respectively. Find the second and third terms of the progression.
respectively. Find the second and third terms of the progression.17 marks
-
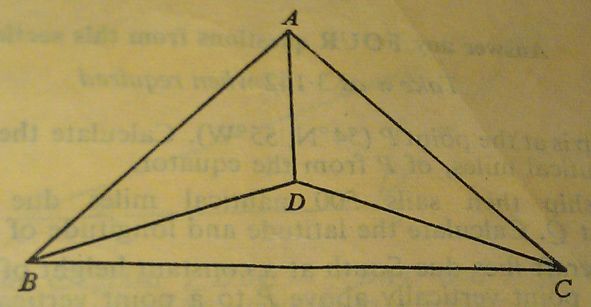
The diagram represents a roof-truss in which AB = AC = 8 m, BC = 11 m, BD = DC and ∠DBC = 20°.
Calculate
(a) the length BD,
(b) the angle ABC,
(c) the length AD.
- Draw the graph of
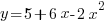 for values of
for values of  from -1 to +4, taking 2 cm as one unit on the x-axis and 1 cm as one unit on the y-axis. From your graph, find the range of values of
from -1 to +4, taking 2 cm as one unit on the x-axis and 1 cm as one unit on the y-axis. From your graph, find the range of values of  for which the function
for which the function 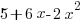 is greater than 6.
is greater than 6.
Using the sane axes and scales, draw the graph of
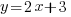 and write down the
and write down the  coordinates of the points of intersection of the two graphs.
coordinates of the points of intersection of the two graphs.if
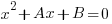 is the quadratic equation of which these
is the quadratic equation of which these  coordinates are the roots, determine the values of
coordinates are the roots, determine the values of 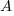 and
and 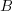 .
.17 marks
- A particle starts from rest at a point A and moves along a straight line, coming to rest again at another point B. During the motion its velocity,
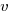 metres per second, after time
metres per second, after time 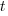 is given by
is given by 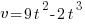 .
.
Calculate:
(a) the time taken for the particle to reach B.
(b) the distance travelled during the first two seconds,
(c) the time taken for the particle to attain its maximum velocity,
(d) the maximum velocity attained,
(e) the maximum acceleration during the motion.
17 marks
Recent Comments