Archive
Median system cpu clock frequency over last 15 years
We are all familiar with graphs showing the growth of cpu clock frequency over time. The data for these plots is based on vendor announcements listing the characteristics of their latest products, and invariably focuses on the product which is the fastest or contains the most transistors or the lowest power consumption.
Some customers buy the cpu with the highest/most/lowest, but many are happy to pay less for, for good enough. What does a graph of average customer cpu clock frequency over time look like?
Vendors sometimes publish general sales figures, but I have never seen one broken down by clock frequency. However, a few sites collect user system data, including:
- A subset of the Linux Counter project data is available. This does not contain explicit date information, but a must-be-later-than date can be inferred from the listed Linux kernel version,
- Hardware for BSD has data going back to December 2014, but there is no obvious way to extract it (I have not tried that hard),
- the BSDstats project (variable website availability) has been collecting data on machines running some derivative of BSD since August 2008; it contains around 200 times more cpu data than the known Linux Counter data. While the raw data is not available, approximately monthly reports are available on the Wayback Machine.
A BSDstats cpu history was obtained using waybackpack to download the available stored cpu summary pages, followed by html2text, and an awk script to extract the cpu frequency/count data.
BSDstats obtains the cpu information via a call to the sysctl command. For many Intel processors, but not AMD processors, the returned string includes the frequency (to see your cpu information on Linux systems type: more /proc/cpu), for instance:
Celeron(R) CPU 2.80GHz | 336 Pentium(R) 4 CPU 3.00GHz | 258 Pentium(R) 4 CPU 2.40GHz | 170 Athlon(tm) 64 Processor 3000+ | 43 Athlon(tm) 64 X2 Dual Core Processor 4200+ | 28 Athlon(tm) 64 Processor 3500+ | 27 |
For simplicity, only those rows containing frequency information were used in this analysis; 67% of the strings explicitly included a frequency (this saved me having to build a table to map AMD cpu strings to their corresponding frequency).
The plot below shows median cpu frequency (in red), along with the top/bottom 10% cpu frequencies, based on the Wayback Machine’s copy of the webpage on a given date, for a total of 2,304,446 cpu identities (code+data):
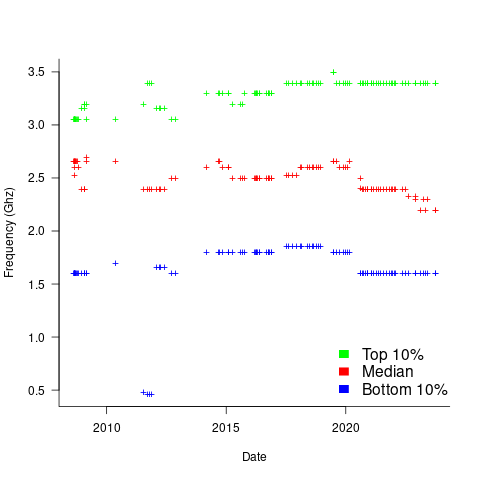
Broadly, the plot shows that cpu frequencies have essentially remained unchanged since 2008, with systems running BSD having a median frequency of 2.5 GHz, with 10% of systems having a frequency over 3.5 GHz, and 10% of systems a frequency below 1.5 GHz.
I was surprised at how many different frequencies were present in the data; often over 50. A look at the large number of different versions of Intel x86 cpus suggests that this is to be expected.
How representative is this sample of BSD systems, compared to the many more systems running Linux and Windows?
This begs the question of what kinds of environments are being compared. Are these desktop systems, local or hosted clusters, cloud systems?
The plot below shows the total number of cpus summarised on each Wayback Machine snapshot (code+data):
A few thousand systems are likely to be personal desktop systems, while the tens of thousands are likely to be clusters or small cloud providers.
Pointers to more data, particularly pre-2000, most welcome.
Instructions that cpus don’t need to support
What instructions can computers do without (an earlier post covered instructions they should support)?
The R in RISC was supposed to stand for Reduced, but in practice almost all the instructions you would expect were supported. What was missing were the really complicated instructions that machines of the time (last 1980s), like the VAX, supported (analysis of instruction set usage showed that these complicated instructions were rarely used; from the compiler perspective the combination sequence of operations supported by these instructions rarely occurred in code).
One instruction that was often missing from the early RISC processors was integer multiply. Compilers were expected to generate a series of instructions that had the same effect. Some of the omitted ‘basic’ instructions got added to later versions of the processors that survived commercially (e.g., SPARC).
The status register is still a common omission from RISC designs (at least for the integer operations). Where is the data showing that in the grand scheme of things (i.e., processor performance running real programs), status registers slow things down? I know that hardware designers don’t like them because they introduce bottlenecks. I don’t recall ever having seen an analysis of instruction set usage targeted at the impact of status registers on generated code. Pointers welcome.
These days, nobody seems to analyze instruction set usage like they did in times past. Perhaps Intel’s marketing and the demise of almost every cpu vendor has dampened enthusiasm for researching new cpu designs. These days most new cpu designs seem to be fashion driven, rather than data driven.
Do computers need registers? An issue that once attracted lots of research was the optimal number of registers for a processor. The minimum number of registers (or temporary storage locations) needed to evaluate an expression was known by 1970. There were various studies of the impact, on code generation, of increasing/decreasing the number of registers available to the compiler. But these studies were done using 1990s era compilers and modern compilers do many more optimizations; whole program optimization ought to be able to make use of many more registers than are probably available on today’s processors (at least I think so, until somebody does a study that shows otherwise). There is a register-less processor that is supposed to be taking the world by storm, sometime soon.
Do computers need to support the IEEE floating-point representation? Logarithmic number systems are starting to be used in various devices, but accuracy remains an issue for some applications.
Main memory: the crucial component that vendors don’t mention
CPU performance hogs the limelight when people discuss the year-on-year increases in computing power that used to occur.
This focus on cpu performance was/is driven by marketing, the people with the money either don’t want customers thinking about the performance impact of main memory size or speed, or want them to treat the processor as the most important component of a computer. Vendors want processor performance to drive customer purchase decisions.
Hardware manufacturers used to entice new customers with low cost machines, containing minimal memory. Once a customer started to use their shiny new computer, they found that it did save them lots of time and money, but also they needed more memory (which could only be brought from the manufacturer and was not cheap).
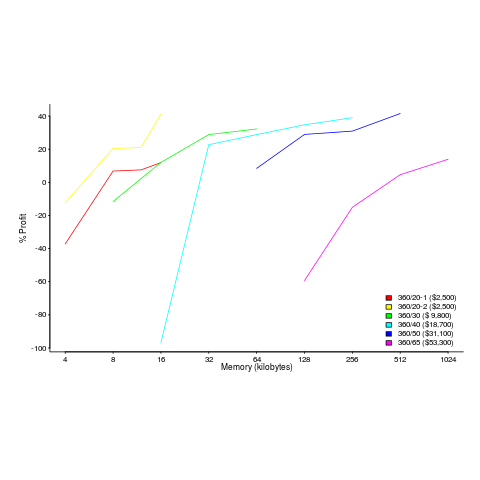
The plot below shows the prices IBM charged for System 360s, in 1966. Anti-trust investigations uncover all kinds of interesting data, like selling low-spec equipment at a loss to entice customers and make life difficult for competitors (code+data for all plots).
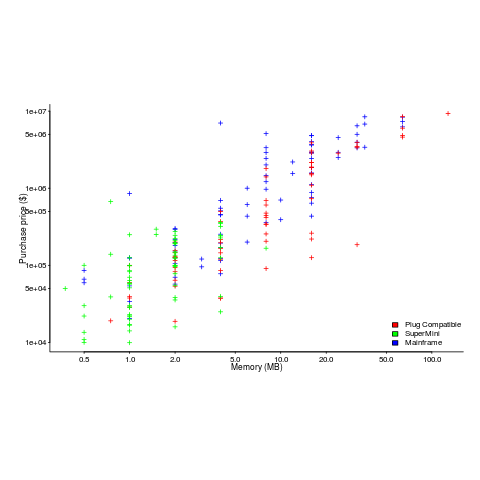
The plot below (data from the 19 Aug 1985 issue of ComputerWorld) shows how the price of computers increased as the minimum about of memory they supported increased.
Yes, in 1985 top end computers came with over 50M of memory; but most customers thought themselves lucky if they had a few megabytes.
If the processor is slow, it just takes longer for programs to run. If the computer does not have enough memory, programs cannot run. For most applications memory requirements are addressed first, followed by processor performance; memory requirements is the number one issue. The optimizations that commercial compilers could perform were limited by the memory capacity of developer machines.
Intel’s main line of business used to be selling memory chips, but these chips became commodity items as more companies entered the market; Intel bet the farm on selling processors and the rest is history. As a seller of a unique product it was/is in Intel’s interest to spend lots of money on marketing the benefits of processor performance; sellers of commodity items (such as memory chips) don’t have nearly as much to gain from generic product marketing, because customers may choose to buy from other sellers (in such markets sellers have to concentrate on marketing themselves).
Memory capacity/speed and cpu speed are two aspects of system performance; they need to be balanced to meet customer drive application requirements. The plot below shows the SPEC cpu integer performance of 4,332 systems running at various clock rates; the colors denote the different peak memory transfer rates of the memory chips in these systems (code+data).
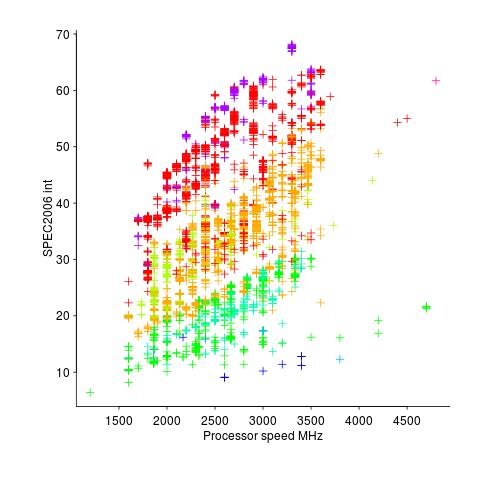
These days (and perhaps in the past, I don’t have any data), memory performance is a much better predictor of system performance, but vendors don’t have an incentive to market this fact.
cpu+FPGA: applications can soon have bespoke instructions
Compiler writers are always frustrated that the cpu they are currently targeting does not contain the one instruction that would enable them to generate really efficient code. If only it were possible to add new instructions to the cpu. Well, it looks like this will soon be possible; Intel have added an on chip FPGA to their Broadwell processor (available circa 2017).
Having custom instructions on a FPGA (they would be loaded at program startup) is not the same as having the instructions on the cpu itself, there will be communication overhead when the data operated on by the custom instruction get transferred back and forth between cpu/FPGA (being on-chip means this will be low). To make the exercise worthwhile the custom instruction has to do something that takes very many cycles on the cpu and either speeds it up or reduces the power consumed (the Catapult project at Microsoft has a rack of FPGA enhanced machines speeding up/reducing the power of matching search engine queries to documents).
A CPU+FPGA is like CPU+GPU, except that FPGAs are programmed at a much lower level, i.e., there is little in the way of abstraction between what the hardware does and what the coder sees.
Does the world need a FPGA attached to their cpu? Most don’t but there are probably a few customers who do, e.g., data centers with systems performing dedicated tasks and anybody into serious bit twiddling. Other considerations include Intel needing to add new bells and whistles to its product so that customers who have been trained over the years to buy the very latest product (which has the largest margins) stay on the buying treadmill. The FPGA is also a differentiator, not that Intel would ever think of AMD as a serious competitor.
Initially the obvious use case is libraries performing commonly occurring functionality. No, not matrix multiple and inverse, FPGA are predominantly integer operation units (there are approaches using non-standard floating-point formats that can be used if your FPGA unit does not have floating-point support).
From the compiler perspective the use case is spotting cpu intensive loops, where all the data can be held on the FPGA until processing is complete. Will there be enough of these loops to make it a worthwhile implementation target? I suspect not. But then I can see many PhDs being written on this topic and one of them could produce a viable implementation that bootstraps itself into one of the popular open source compilers.
Interpreters have to do a lot of housekeeping work. Perhaps programs written in Java or R could be executed on the FPGA that uses the cpu as a slave processor. It is claimed that most R programs spend their time in library functions that have been implemented in C and Fortran, but I’m seeing more and more code that appears to be all R. For some programs an R-machine implemented in hardware could produce orders of magnitude speed improvements.
The next generation of cryptocurrency proof-of-work algorithms are being designed to be memory intensive, so they cannot be efficiently implemented using ASIC-proof (this prevents mining being concentrated in a few groups who have built bespoke mining operations). The analysis I have seen is based on ‘conventional’ cpu and ASIC designs. A cpu+FPGA is a very different kind of beast and one that might require another round of cryptocurrency design.
These cpu+FPGA processors have the potential to dramatically upend existing approaches to structuring programs. Very interesting times ahead!
Hardware variability may be greater than algorithmic improvement
I’m giving a talk at COW 39 this week and it is more user friendly to include links in this summary than link to a pdf of the slides (which actually looks horrible).
Microelectronic fabrication has now reached the point where it etches and deposits handfuls of atoms (around 20 or so). One consequence of working with such a small number of atoms is that variations in the fabrication process (e.g., plus or minus a few atoms here and there) can have a significant impact on component characteristics, e.g., a transistor consumes more/less power or can be switched faster/slower. It might be argued that things will average out over the few hundred+ million components inside a device and that all devices will be essentially the same; measurements show that in practice there is a lot of variation across the devices.
Short version: Some properties of supposedly identical microelectronic devices now vary by around 10% and this variability is likely to get larger in the future.
Nearly all published papers involving computer system power measurement are based on measuring a single system. Many of the claimed algorithmic improvements are less than 10%, i.e., less than the expected variation in power consumption across supposedly identical devices/systems. These days any empirical paper involving power consumption has to include measurements from many devices/systems if any credibility is to be given to the findings.
The following measurement data has been found while researching for a book (code and data used for talk); a beta version of the pdf will be available for download real soon now.
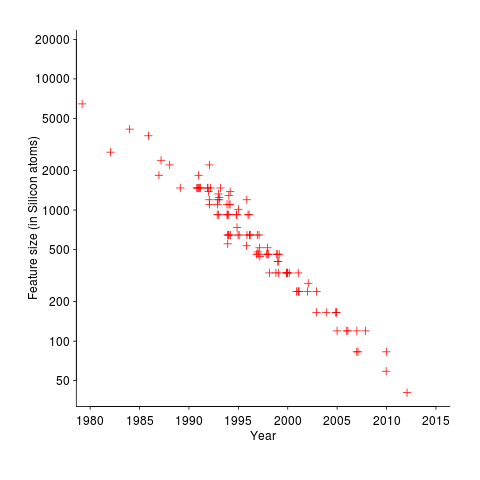
The following plot shows feature size, in Silicon atoms, of released microprocessors. Data from Danowitz et al.
A study by Wanner, Apte, Balani, Gupta and Srivastava measured the power consumed by 10 separate Amtel SAM3U microcontrollers at various temperatures (embedded processors get used in a wide range of environments). The following plot shows how power consumption varied between processors at different temperatures when idling and executing. The relationship between the power characteristics of different processors changes with temperature; a large amount when idling and a little bit when executing.
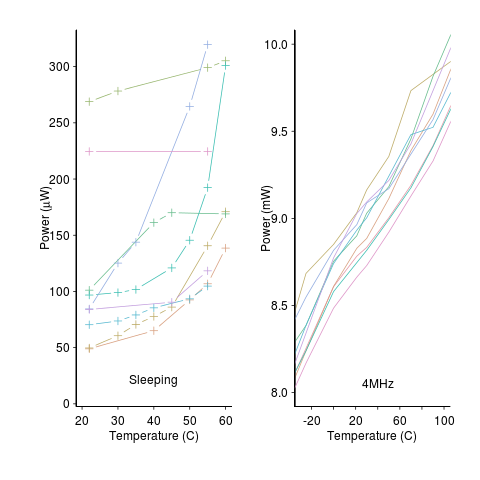
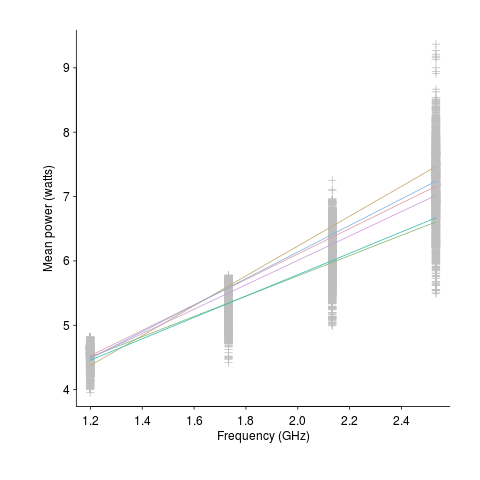
A study by Balaji, McCullough, Gupta and Agarwal measured the power consumption of six different Intel Core i5-540M processors, running at various frequencies, executing the SPEC2000 benchmark. The lines in the following plot were fitted to the data (grey crosses) using linear regression. The relationship between the power characteristics of different processors changes with clock frequency.
A study by Bircher measured power consumption of various system components, of an Intel server containing four Pentium 4 Xeons, when executing the SPEC CPU2006 benchmark. The power distribution for mobile devices would show the screen being the largest user of power, but I don’t have that data).
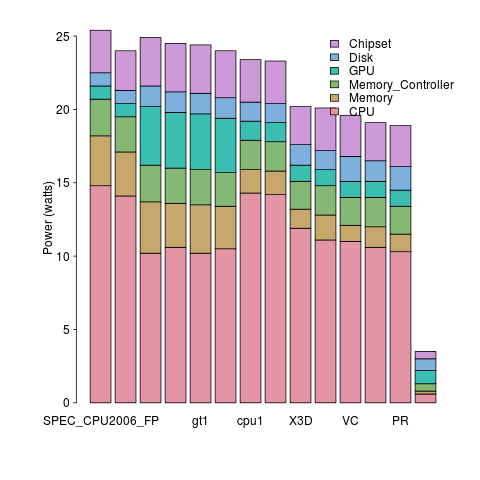
A study by Bircher measured memory (blue) and cpu (red) power consumption, in watts, executing the SPEC CPU2006 benchmarks. No point optimizig cpu power if over half the total power is consumed by memory.
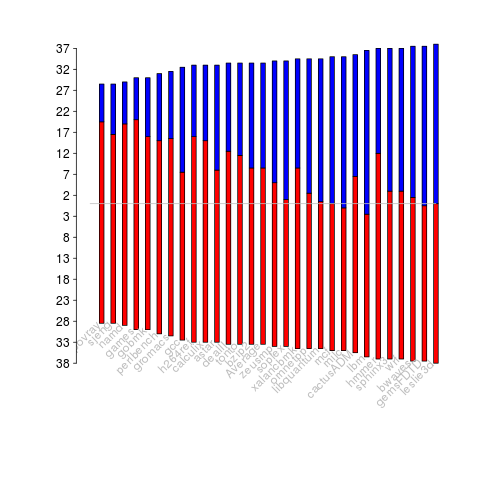
A study by Krevat, Tucek and Ganger measured the performance of then modern disk drives originally sold in 2002 (left) and 2006 (right). Different colors showing through on the right indicates that some discs have different performance characteristics than the others (faster performance -> less time -> less power, i.e., I don’t have power data for disk differences)
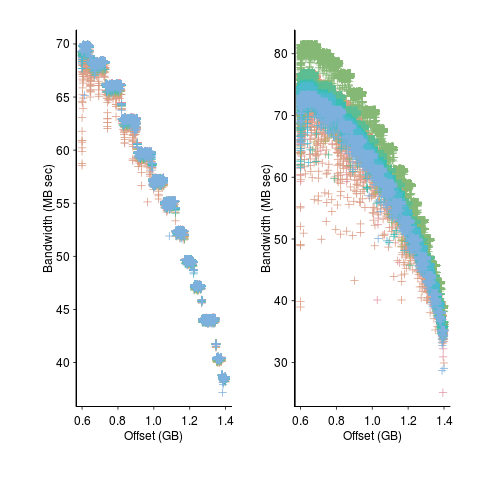
A study by Kalibera et al executed a benchmark 2,048 times followed by system reboot, repeated 10 times. Performance is consistent within a particular reboot, but not across them.
The following plot is in the slide deck and is included here as a teaser (i.e., more later). It shows data for 2,386 processors (x-axis is slowdown, y-axis clock frequency, top right legends max power), which thanks to Barry is now publicly available (or at least will be once some web details are sorted out).
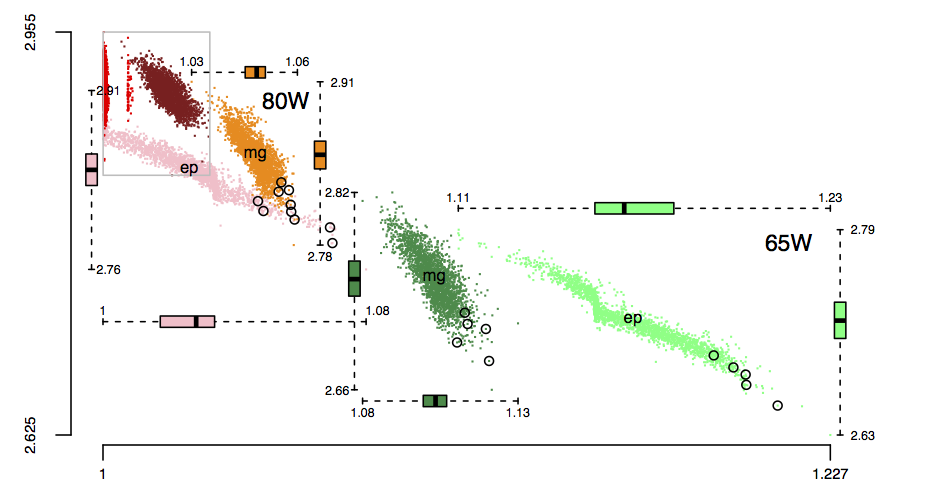
Unreliable cpus and memory: The end result of Moore’s law?
Where is the evolution of commodity cpu and memory chips going to take its customers? I think the answer is cheap and unreliable products (just like many household appliances are priced low and have a short expected lifetime).
We have had the manufacturer-customer win-win phase of Moore’s law and I think we are now entering the win-loose phase.
The reason chip manufacturers, such as Intel, invest so heavily on continually shrinking dies is the same reason all companies invest, they expect to get a good return on their investment. The cost of processing the wafer from which individual chips are cut is more or less constant, reducing the size of a chip enables more to fitted on the same wafer, giving more product to sell for more or less the same wafer processing cost.
The fact that dies with smaller feature sizes have reduce power consumption and can run at faster clock speeds (up until around 10 years ago) is a secondary benefit to manufacturers (it created a reason for customers to replace what they already owned with a newer product); chip manufacturers would still have gone down the die shrink path if these secondary benefits had not existed, but perhaps at a slower rate. Customers saw, or were marketed, this strinkage story as one of product improvement for their benefit rather than as one of unit cost reduction for Intel’s benefit (Intel is the end-customer facing company that pumped billions into marketing).
Until recently both manufacturer and customer have benefited from die shrinks through faster cpus/lower power consumption and lower unit cost.
A problem that was rarely encountered outside of science fiction a few decades ago is now regularly encountered by all owners of modern computers, cosmic rays (plus more local source of ‘rays’) altering the behavior of running programs (4 GB of RAM is likely to experience a single bit-flip once every 33 hours of operation). As die shrink continues this problem will get worse. Another problem with ever smaller transistors is their decreasing mean time to failure (very technical details); we have seen expected chip lifetimes drop from 10 years to 7 and now less and decreasing.
Decreasing chip lifetimes is actually good for the manufacturer, it creates a reason for customers to buy a new product. Buying a new computer every 2-3 years has been accepted practice for many years (because the new ones were much better). Are we, the customer, in danger of being led to continue with this ‘accepted practice’ (because computers reliability is poor)?
Surely it is to the customer’s advantage to not buy devices that contain chips with even smaller features? Is it only the manufacturer that will obtain a worthwhile benefit from future die shrinks?
Programs spent a lot of time repeating themselves
Inexperienced software developers are always surprised that programs used by lots of people can contain many apparently non-trivial faults and yet continue to operate satisfactorily; experienced developers become familiar with this state of affairs and tend to shrug their shoulders. I have previously written about how software is remarkably fault tolerant. I think this fault tolerance is telling us something important about the characteristics of software and while I have some ideas about what it might be I don’t yet have a good handle (or data) on what is going on to lay out my argument.
In this article I’m going to talk about another characteristic of program execution which I think is connected to program fault tolerance and is also very surprising.
Software differs from hardware in that for a given set of inputs a program will always produce the same output, it will not wear out like hardware and eventually do something different (to simplify things I’m ignoring the possible consequences of uninitialized variables and treating any timing dependencies as part of the input set). So for a fault to be observed different input is required (assuming one exists and none appeared for the first input set).
I used to assume that during a program’s execution the basic cpu operations (e.g., binary arithmetic and bitwise operations) processed a huge number of different combinations of input values (e.g., there are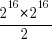 
combinations of input value for a 16-bit add operation) and was very surprised to find out this is not the case. For many programs around 80% of all executed instructions are repeat instructions, that is a given instruction, such as add, operates on the same combinations of input values that it has previously operated on (while executing the program) to generate an output value that is identical to the one previously generated from these input values. If we count the number of static instructions in the program (i.e., the number of assembly instructions in a listing of the disassembled executable program) then 20% of them account for 90% of the repeated instructions; so a small amount of code (i.e., 20%) is not only responsible for most dynamically executed instructions but around 72% (i.e., 80%*90%) of these instructions repeat previous computations. If a large percentage of a what goes on internally within a program is repetition is it any surprise that once it works for a reasonable set of inputs it will probably work on other inputs?
Hang on you say, perhaps the percentage of repeat instructions is very high for a given set of external input values (e.g., a file to compress, compile or display as a jpeg) but there is a lot of variation in the set of repeat instructions between different external inputs. Measurements suggest this is not the case, with around 20% of dynamic instructions having input values that can be traced to external program input (12-30% come from globally initialized variables and the rest are generated internally).
There is a technical detail that reduces the repeat instruction percentages given about by a factor of two; researchers always like to give the most favorable numbers and for this discussion we need to make a distinction between local repetition which counts one instruction and its inputs/outputs at a particular point in the code and global repetition which counts all instructions of a given kind irrespective of where they occur in the code. A discussion of fault behavior needs to look at local repetition, not global repetition; there is a factor of two difference in the dynamic percentage and some reduction in the percentage of static instructions involved.
Sometimes the term redundant computation is used, as if the cpu should remember what happened last time it executed an instruction with a particular set of inputs and reuse the answer it got last time. Researchers have proposed caching the results of executing an instruction with a given set of input values and speeding things up or saving power by reusing previous results rather than recalculating them (a possible speedup of 13% on SPEC95 is claimed for a reuse buffer containing 4096 entries).
So a small percentage of the instructions in a program account for most of the execution time (a generally known characteristic) and around 30% of the executed instructions operate on input values they have processed before to produce output they have produced before (to the extent that a cache containing a few thousand entries is big enough to hold the a large percentage of the duplicates). If encountering a new fault requires different execution behavior to occur then having a large percentage of a program always doing the same thing (i.e., same input values same output value) will have a significant impact on the likelihood of encountering a fault. Part of the reason programs are fault tolerant is because external input values don’t have a big an impact on program behavior as we might have thought.
Researchers have also investigated repeats involving units larger than one instruction, such as sub-blocks (a sequence of instructions smaller than a basic block) and even complete functions or just the mathematical ones.
The raw data is obtained using cpu simulators to monitor programs as they are executed, logging the values read as input by an instruction and the value generated as output (in most cases the values are read from registers and written to a register). A single study might log billions of instructions from the SPEC benchmark.
Superoptimizers are back in vogue
There has always been the need for a few developer with in-depth knowledge of a particular cpu architecture to sit down and think very hard about how best to implement a snippet of code performing some operation in assembly language, e.g., library implementors wanting the tightest code for a critical inner loop or compiler writers who need to map from intermediate code to machine code.
In 1987 Massalin published his now famous paper that introduced the term Superoptimizer; a program that enumerates all possible combinations of instruction sequences until the shortest/fastest one producing the desired output from the given input is found (various heuristics were used to prune the search space e.g., only considering 15 or so opcodes, and the longest sequence it ever generated contained 12 instructions).
While the idea was widely talked about it never caught on in practice (a special purpose branch eliminator was produced for GCC; Hacker’s Delight also includes a stand alone system). Perhaps the guild of mindbogglingly-obtuse-but-fast-instruction-sequences black-balled it (apprentices have to spend several years doing nothing but writing assembly code for their chosen architecture, thinking about how to make it go faster and/or be shorter and only talk to other apprentices/members and communicate with non-converts exclusively about their latest neat sequence), or perhaps it was just a case of not invented here (writing machine code used to be something that even run of the mill developers got to do every now and again), or perhaps it was not considered cost effective to build a superoptimizer for a given project (I don’t know of anyone offering a generic tool that could be tailored for specific cases) or perhaps developers were happy to just ride the wave of continually faster processors.
It was not until 2008 with Bansal’s thesis that superoptimizer research started to take off (as in paper publication rate increased from once every five years to more than one a year). Bansal found a new market, binary translation i.e., translating the binary of a program built to run on one kind of cpu to run on a different kind of cpu, for instance the Mac 68K emulator.
Bansal and other researchers’ work was oriented towards relatively short instruction sequences. To be really useful some way of handling longer sequences was needed.
A few days ago Stochastic Superoptimization arrived on the scene (or rather a paper describing it became available for download). Schkufza, Sharma and Aiken use Markov chain Monte Carlo methods to sample the possible instruction sequences rather than generating all of them. The paper gives a 116 instruction example from which the author’s tool removed 16 lines to produce code that went 1.6 times faster (only 30 ‘core’ instructions were given in paper); what is also very interesting is that the tool operates on compiler generated output (gcc/llvm), suggesting the usage build program, profile it and then stochastic superoptimize the hot spots.
Markov chains and Monte Carlo methods are trendy topics that researchers like to write about, so we will certainly see more papers in this area.
These days few developers have had hands on experience with machine code, so the depth of expertise that was once easy to find is now rare, processors have many more weird and wonderful instructions often interacting with older instructions in obscure ways and the cpu architecture landscape continues to change regularly. The time may have arrived for Superoptimizers to be widely used by industry.
Of course superoptimizers can work at any level of abstraction, including expression trees built directly from some complicated floating-point calculation that needs to be optimized for accuracy or speed.
Recent Comments