Archive
The C++ committee has taken off its ball and chain
A step change in the approach to updates and additions to the C++ Standard occurred at the recent WG21 meeting, or rather a change that has been kind of going on for a few meetings has been documented and discussed. Two bullet points at the start of “C++ Stability, Velocity, and Deployment Plans [R2]”, grab reader’s attention:
● Is C++ a language of exciting new features?
● Is C++ a language known for great stability over a long period?
followed by the proposal (which was agreed at the meeting): “The Committee should be willing to consider the design / quality of proposals even if they may cause a change in behavior or failure to compile for existing code.”
We have had 30 years of C++/C compatibility (ok, there have been some nibbling around the edges over the last 15 years). A remarkable achievement, thanks to Bjarne Stroustrup over 30+ years and 64 full-week standards’ meetings (also, Tom Plum and Bill Plauger were engaged in shuttle diplomacy between WG14 and WG21).
The C/C++ superset/different issue has a long history.
In the late 1980s SC22 (the top-level ISO committee for programming languages) asked WG14 (the C committee) whether a standard should be created for C++, and if so did WG14 want to create it. WG14 considered the matter at its April 1989 meeting, and replied that in its view a standard for C++ was worth considering, but that the C committee were not the people to do it.
In 1990, SC22 started a study group to look into whether a working group for C++ should be created and in the U.S. X3 (the ANSI committee responsible for Information processing systems) set up X3J16. The showdown meeting of what would become WG21, was held in London, March 1992 (the only ISO C++ meeting I have attended).
The X3J16 people were in London for the ISO meeting, which was heated at times. The two public positions were: 1) work should start on a standard for C++, 2) C++ was not yet mature enough for work to start on a standard.
The, not so public, reason given for wanting to start work on a standard was to stop, or at least slow down, changes to the language. New releases, rumored and/or actual, of Cfront were frequent (in a pre-Internet time sense). Writing large applications in a version of C++ that was replaced with something sightly different six months later had developers in large companies pulling their hair out.
You might have thought that compiler vendors would be happy for the language to be changing on a regular basis; changes provide an incentive for users to pay for compiler upgrades. In practice the changes were so significant that major rework was needed by somebody who knew what they were doing, i.e., expensive people had to be paid; vendors were more used to putting effort into marketing minor updates. It was claimed that implementing a C++ compiler required seven times the effort of implementing a C compiler. I have no idea how true this claim might have been (it might have been one vendor’s approximate experience). In the 1980s everybody and his dog had their own C compiler and most of those who had tried, had run into a brick wall trying to implement a C++ compiler.
The stop/slow down changing C++ vs. let C++ “fulfill its destiny” (a rallying call from the AT&T rep, which the whole room cheered) finally got voted on; the study group became a WG (I cannot tell you the numbers; the meeting minutes are not online and I cannot find a paper copy {we had those until the mid/late-90s}).
The creation of WG21 did not have the intended effect (slowing down changes to the language); Stroustrup joined the committee and C++ evolution continued apace. However, from the developers’ perspective language change did slow down; Cfront changes stopped because its code was collapsing under its own evolutionary weight and usable C++ compilers became available from other vendors (in the early days, Zortech C++ was a major boost to the spread of usage).
The last WG21 meeting had 140 people on the attendance list; they were not all bored consultants looking for a creative outlet (i.e., exciting new features), but I’m sure many would be happy to drop the ball-and-chain (otherwise known as C compatibility).
I think there will be lots of proposals that will break C compatibility in one way or another and some will make it into a published standard. The claim will be that the changes will make life easier for future C++ developers (a claim made by proponents of every language, for which there is zero empirical evidence). The only way of finding out whether a change has long term benefit is to wait a long time and see what happens.
The interesting question is how C++ compiler vendors will react to breaking changes in the language standard. There are not many production compilers out there these days, i.e., not a lot of competition. What incentive does a compiler vendor have to release a version of their compiler that will likely break existing code? Compiler validation, against a standard, is now history.
If WG21 make too many breaking changes, they could find C++ vendors ignoring them and developers asking whether the ISO C++ standards’ committee is past its sell by date.
The first compiler was implemented in itself
I have been reading about the world’s first actual compiler (i.e., not a paper exercise), described in Corrado Böhm’s PhD thesis (French version from 1954, an English translation by Peter Sestoft). The thesis, submitted in 1951 to the Federal Technical University in Zurich, takes some untangling; when you are inventing a new field, ideas tend to be expressed using existing concepts and terminology, e.g., computer peripherals are called organs and registers are denoted by the symbol 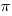 .
.
Böhm had work with Konrad Zuse and must have known about his language, Plankalkül. The language also has a APL feel to it (but without the vector operations).
Böhm’s language does not have a name, his thesis is really about translating mathematical expressions to machine code; the expressions are organised by what we today call basic blocks (Böhm calls them groups). The compiler for the unnamed language (along with a loader) is written in itself; a Java implementation is being worked on.
Böhm’s work is discussed in Donald Knuth’s early development of programming languages, but there is nothing like reading the actual work (if only in translation) to get a feel for it.
Update (3 days later): Correspondence with Donald Knuth.
Update (3 days later): A January 1949 memo from Haskell Curry (he of Curry fame and more recently of Haskell association) also uses the term organ. Might we claim, based on two observations on different continents, that it was in general use?
Grace Hopper: Manager, after briefly being a programmer
In popular mythology Grace Hopper is a programmer who wrote one of the first compilers. I think the reality is that Hopper did some programming, but quickly moved into management; a common career path for freshly minted PhDs and older people entering computing (Hopper was in her 40s when she started); her compiler management work occurred well after many other compilers had been written.
What is the evidence?
Hopper is closely associated with Cobol. There is a lot of evidence for at least 28 compilers in 1957, well before the first Cobol compiler (can a compiler written after the first 28 be called one of the first?)
The A-0 tool, which Hopper worked on as a programmer in 1951-52, has been called a compiler. However, the definition of Compile used sounds like today’s assembler and the definition of Assemble used sounds like today’s link-loader (also see: section 7 of Digital Computers – Advanced Coding Techniques for Hopper’s description of what A-2, a later version, did).
The ACM’s First Glossary of Programming Terminology, produced by a committee chaired by Hopper in June 1954.
Routine – a set of coded instructions arranged in proper sequence to direct the computer to perform a desired operation or series of operations. See also Subroutine.
Compiler (Compiling Routine) – an executive routine which, before the desired computation is started, translates a program expressed in pseudo-code into machine code (or into another pseudo-code for further translation by an interpreter). In accomplishing the translation, the compiler may be required to:
…
Assemble – to integrate the subroutines (supplied, selected, or generated) into the main routine, i.e., to:
Adapt – to specialize to the task at hand by means of preset parameters.
Orient – to change relative and symbolic addresses to absolute form.
Incorporate – to place in storage.
Hopper’s name is associated with work on the MATH-MATIC and ARITH-MATIC Systems, but her name does not appear in the list of people who wrote the manual in 1957. A programmer working on these systems is likely to have been involved in producing the manual.
After the A-0 work, all of Hopper’s papers relate to talks she gave, committees she sat on and teams she led, i.e., the profile of a manager.
Whole-program optimization: there’s gold in them hills
Information is the life-blood of compiler optimization and compiler writers are always saying “If only this-or-that were known, we could do this optimization.”
Burrowing down the knowing this-or-that rabbit-hole leads to requiring that code generation be delayed until link-time, because it is only at link-time that all the necessary information is available.
Whole program optimization, as it is known, has been a reality in the major desktop compilers for several years, in part because computers having 64G+ of memory have become generally available (compiler optimization has always been limited by the amount of memory available in developer computers). By reality, I mean compilers support whole-program-optimization flags and do some optimizations that require holding a representation of the entire program in memory (even Microsoft, not a company known for leading edge compiler products {although they have leading edge compiler people in their research group} supports an option having this name).
It is still early days for optimizations that are “whole-program”, rather like the early days of code optimization (when things like loop unrolling were leading edge and even constant folding was not common).
An annoying developer characteristic is writing code that calls a function every five statements, on average. Calling a function means that all those potentially reusable values that have been loaded into registers, before the call, cannot be safely used after the call (figuring out whether it is worth saving/restoring around the call is hard; yes developers, its all your fault that us compiler writers have such a tough job :-P).
Solutions to the function call problem include inlining and flow-analysis to figure out the consequences of the call. However, the called function calls other functions which in-turn burrow further down the rabbit hole.
With whole-program optimization, all the code is available for analysis; given enough memory and processor time lots of useful information can be figured out. Most functions are only called once, so there are lots of savings to be had from using known parameter values (many are numeric literals) to figure out whether an if-statement is necessary (i.e., is dead code) and how many times loops iterate.
More fully applying known techniques is the obvious easy use-case for whole-program optimization, but the savings probably won’t be that big. What about new techniques that previously could not even be attempted?
For instance, walking data structures until some condition is met is a common operation. Loading the field/member being tested and the next/prev field, results in one or more cache lines being filled (on the assumption that values adjacent in storage are likely to be accessed in the immediate future). However, data structures often contain many fields, only a few of which need to be accessed during the search process, when the next value needed is in another instance of the struct/record/class it is unlikely to already be available in the loaded cache line. One useful optimization is to split the data structure into two structures, one holding the fields accessed during the iterative search and the other holding everything else. This data-remapping means that cache lines are more likely to contain the next value accessed approaches increases the likelihood that cache lines will hold a values needed in the near future; the compiler looks after the details. Performance gains of 27% have been reported
One study of C++ found that on average 12% of members were dead, i.e., never accessed in the code. Removing these saved 4.4% of storage, but again the potential performance gain comes from improve the cache hit ratio.
The row/column storage layout of arrays is not cache friendly, using Morton-order layout can have a big performance impact.
There are really really big savings to be had by providing compilers with a means of controlling the processors caches, e.g., instructions to load and flush cache lines. At the moment researchers are limited to simulations show that substantial power savings+some performance gain are possible.
Go forth and think “whole-program”.
Evidence for 28 possible compilers in 1957
In two earlier posts I discussed the early compilers for languages that are still widely used today and a report from 1963 showing how nothing has changed in programming languages
The Handbook of Automation Computation and Control Volume 2, published in 1959, contains some interesting information. In particular Table 23 (below) is a list of “Automatic Coding Systems” (containing over 110 systems from 1957, or which 54 have a cross in the compiler column):
Computer System Name or Developed by Code M.L. Assem Inter Comp Oper-Date Indexing Fl-Pt Symb. Algeb.
Acronym
IBM 704 AFAC Allison G.M. C X Sep 57 M2 M 2 X
CAGE General Electric X X Nov 55 M2 M 2
FORC Redstone Arsenal X Jun 57 M2 M 2 X
FORTRAN IBM R X Jan 57 M2 M 2 X
NYAP IBM X Jan 56 M2 M 2
PACT IA Pact Group X Jan 57 M2 M 1
REG-SYMBOLIC Los Alamos X Nov 55 M2 M 1
SAP United Aircraft R X Apr 56 M2 M 2
NYDPP Servo Bur. Corp. X Sep 57 M2 M 2
KOMPILER3 UCRL Livermore X Mar 58 M2 M 2 X
IBM 701 ACOM Allison G.M. C X Dec 54 S1 S 0
BACAIC Boeing Seattle A X X Jul 55 S 1 X
BAP UC Berkeley X X May 57 2
DOUGLAS Douglas SM X May 53 S 1
DUAL Los Alamos X X Mar 53 S 1
607 Los Alamos X Sep 53 1
FLOP Lockheed Calif. X X X Mar 53 S 1
JCS 13 Rand Corp. X Dec 53 1
KOMPILER 2 UCRL Livermore X Oct 55 S2 1 X
NAA ASSEMBLY N. Am. Aviation X
PACT I Pact Groupb R X Jun 55 S2 1
QUEASY NOTS Inyokern X Jan 55 S
QUICK Douglas ES X Jun 53 S 0
SHACO Los Alamos X Apr 53 S 1
SO 2 IBM X Apr 53 1
SPEEDCODING IBM R X X Apr 53 S1 S 1
IBM 705-1, 2 ACOM Allison G.M. C X Apr 57 S1 0
AUTOCODER IBM R X X X Dec 56 S 2
ELI Equitable Life C X May 57 S1 0
FAIR Eastman Kodak X Jan 57 S 0
PRINT I IBM R X X X Oct 56 82 S 2
SYMB. ASSEM. IBM X Jan 56 S 1
SOHIO Std. Oil of Ohio X X X May 56 S1 S 1
FORTRAN IBM-Guide A X Nov 58 S2 S 2 X
IT Std. Oil of Ohio C X S2 S 1 X
AFAC Allison G.M. C X S2 S 2 X
IBM 705-3 FORTRAN IBM-Guide A X Dec 58 M2 M 2 X
AUTOCODER IBM A X X Sep 58 S 2
IBM 702 AUTOCODER IBM X X X Apr 55 S 1
ASSEMBLY IBM X Jun 54 1
SCRIPT G. E. Hanford R X X X X Jul 55 Sl S 1
IBM 709 FORTRAN IBM A X Jan 59 M2 M 2 X
SCAT IBM-Share R X X Nov 58 M2 M 2
IBM 650 ADES II Naval Ord. Lab X Feb 56 S2 S 1 X
BACAIC Boeing Seattle C X X X Aug 56 S 1 X
BALITAC M.I.T. X X X Jan 56 Sl 2
BELL L1 Bell Tel. Labs X X Aug 55 Sl S 0
BELL L2,L3 Bell Tel. Labs X X Sep 55 Sl S 0
DRUCO I IBM X Sep 54 S 0
EASE II Allison G.M. X X Sep 56 S2 S 2
ELI Equitable Life C X May 57 Sl 0
ESCAPE Curtiss-Wright X X X Jan 57 Sl S 2
FLAIR Lockheed MSD, Ga. X X Feb 55 Sl S 0
FOR TRANSIT IBM-Carnegie Tech. A X Oct 57 S2 S 2 X
IT Carnegie Tech. C X Feb 57 S2 S 1 X
MITILAC M.I.T. X X Jul 55 Sl S 2
OMNICODE G. E. Hanford X X Dec 56 Sl S 2
RELATIVE Allison G.M. X Aug 55 Sl S 1
SIR IBM X May 56 S 2
SOAP I IBM X Nov 55 2
SOAP II IBM R X Nov 56 M M 2
SPEED CODING Redstone Arsenal X X Sep 55 Sl S 0
SPUR Boeing Wichita X X X Aug 56 M S 1
FORTRAN (650T) IBM A X Jan 59 M2 M 2
Sperry Rand 1103A COMPILER I Boeing Seattle X X May 57 S 1 X
FAP Lockheed MSD X X Oct 56 Sl S 0
MISHAP Lockheed MSD X Oct 56 M1 S 1
RAWOOP-SNAP Ramo-Wooldridge X X Jun 57 M1 M 1
TRANS-USE Holloman A.F.B. X Nov 56 M1 S 2
USE Ramo-Wooldridge R X X Feb 57 M1 M 2
IT Carn. Tech.-R-W C X Dec 57 S2 S 1 X
UNICODE R Rand St. Paul R X Jan 59 S2 M 2 X
Sperry Rand 1103 CHIP Wright A.D.C. X X Feb 56 S1 S 0
FLIP/SPUR Convair San Diego X X Jun 55 SI S 0
RAWOOP Ramo-Wooldridge R X Mar 55 S1 1
8NAP Ramo-Wooldridge R X X Aug 55 S1 S 1
Sperry Rand Univac I and II AO Remington Rand X X X May 52 S1 S 1
Al Remington Rand X X X Jan 53 S1 S 1
A2 Remington Rand X X X Aug 53 S1 S 1
A3,ARITHMATIC Remington Rand C X X X Apr 56 SI S 1
AT3,MATHMATIC Remington Rand C X X Jun 56 SI S 2 X
BO,FLOWMATIC Remington Rand A X X X Dec 56 S2 S 2
BIOR Remington Rand X X X Apr 55 1
GP Remington Rand R X X X Jan 57 S2 S 1
MJS (UNIVAC I) UCRL Livermore X X Jun 56 1
NYU,OMNIFAX New York Univ. X Feb 54 S 1
RELCODE Remington Rand X X Apr 56 1
SHORT CODE Remington Rand X X Feb 51 S 1
X-I Remington Rand C X X Jan 56 1
IT Case Institute C X S2 S 1 X
MATRIX MATH Franklin Inst. X Jan 58
Sperry Rand File Compo ABC R Rand St. Paul Jun 58
Sperry Rand Larc K5 UCRL Livermore X X M2 M 2 X
SAIL UCRL Livermore X M2 M 2
Burroughs Datatron 201, 205 DATACODEI Burroughs X Aug 57 MS1 S 1
DUMBO Babcock and Wilcox X X
IT Purdue Univ. A X Jul 57 S2 S 1 X
SAC Electrodata X X Aug 56 M 1
UGLIAC United Gas Corp. X Dec 56 S 0
Dow Chemical X
STAR Electrodata X
Burroughs UDEC III UDECIN-I Burroughs X 57 M/S S 1
UDECOM-3 Burroughs X 57 M S 1
M.I.T. Whirlwind ALGEBRAIC M.I.T. R X S2 S 1 X
COMPREHENSIVE M.I.T. X X X Nov 52 Sl S 1
SUMMER SESSION M.I.T. X Jun 53 Sl S 1
Midac EASIAC Univ. of Michigan X X Aug 54 SI S
MAGIC Univ. of Michigan X X X Jan 54 Sl S
Datamatic ABC I Datamatic Corp. X
Ferranti TRANSCODE Univ. of Toronto R X X X Aug 54 M1 S
Illiac DEC INPUT Univ. of Illinois R X Sep 52 SI S
Johnniac EASY FOX Rand Corp. R X Oct 55 S
Norc NORC COMPILER Naval Ord. Lab X X Aug 55 M2 M
Seac BASE 00 Natl. Bur. Stds. X X
UNIV. CODE Moore School X Apr 55 |
Chart Symbols used:
Code R = Recommended for this computer, sometimes only for heavy usage. C = Common language for more than one computer. A = System is both recommended and has common language. Indexing M = Actual Index registers or B boxes in machine hardware. S = Index registers simulated in synthetic language of system. 1 = Limited form of indexing, either stopped undirectionally or by one word only, or having certain registers applicable to only certain variables, or not compound (by combination of contents of registers). 2 = General form, any variable may be indexed by anyone or combination of registers which may be freely incremented or decremented by any amount. Floating point M = Inherent in machine hardware. S = Simulated in language. Symbolism 0 = None. 1 = Limited, either regional, relative or exactly computable. 2 = Fully descriptive English word or symbol combination which is descriptive of the variable or the assigned storage. Algebraic A single continuous algebraic formula statement may be made. Processor has mechanisms for applying associative and commutative laws to form operative program. M.L. = Machine language. Assem. = Assemblers. Inter. = Interpreters. Compl. = Compilers. |
Are the compilers really compilers as we know them today, or is this terminology that has not yet settled down? The computer terminology chapter refers readers interested in Assembler, Compiler and Interpreter to the entry for Routine:
“Routine. A set of instructions arranged in proper sequence to cause a computer to perform a desired operation or series of operations, such as the solution of a mathematical problem.
…
Compiler (compiling routine), an executive routine which, before the desired computation is started, translates a program expressed in pseudo-code into machine code (or into another pseudo-code for further translation by an interpreter).
…
Assemble, to integrate the subroutines (supplied, selected, or generated) into the main routine, i.e., to adapt, to specialize to the task at hand by means of preset parameters; to orient, to change relative and symbolic addresses to absolute form; to incorporate, to place in storage.
…
Interpreter (interpretive routine), an executive routine which, as the computation progresses, translates a stored program expressed in some machine-like pseudo-code into machine code and performs the indicated operations, by means of subroutines, as they are translated. …”
The definition of “Assemble” sounds more like a link-load than an assembler.
When the coding system has a cross in both the assembler and compiler column, I suspect we are dealing with what would be called an assembler today. There are 28 crosses in the Compiler column that do not have a corresponding entry in the assembler column; does this mean there were 28 compilers in existence in 1957? I can imagine many of the languages being very simple (the fashionability of creating programming languages was already being called out in 1963), so producing a compiler for them would be feasible.
The citation given for Table 23 contains a few typos. I think the correct reference is: Bemer, Robert W. “The Status of Automatic Programming for Scientific Problems.” Proceedings of the Fourth Annual Computer Applications Symposium, 107-117. Armour Research Foundation, Illinois Institute of Technology, Oct. 24-25, 1957.
Hedonism: The future economics of compiler development
In the past developers paid for compilers, then gcc came along (followed by llvm) and now a few companies pay money to have a bunch of people maintain/enhance/support a new cpu; developers get a free compiler. What will happen once the number of companies paying money shrinks below some critical value?
The current social structure has an authority figure (ISO committees for C and C++, individuals or companies for other languages) specifying the language, gcc/llvm people implementing the specification and everybody else going along for the ride.
Looking after an industrial strength compiler is hard work and requires lots of know-how; hobbyists have little chance of competing against those paid to work full time. But as the number of companies paying for support declines, the number of people working full-time on the compilers will shrink. Compiler support will become a part-time job or hobby.
What are the incentives for a bunch of people to get together and spend their own time maintaining a compiler? One very powerful incentive is being able to decide what new language features the compiler will support. Why spend several years going to ISO meetings arguing with everybody about whether the next version of the standard should support your beloved language construct, it’s quicker and easier to add it directly to the compiler (if somebody else wants their construct implemented, let them write the code).
The C++ committee is populated by bored consultants looking for an outlet for their creative urges (the production of 1,600 page documents and six extension projects is driven by the 100+ people who attend meetings; a lot fewer people would produce a simpler C++). What is the incentive for those 100+ (many highly skilled) people to attend meetings, if the compilers are not going to support the specification they produce? Cut out the middle man (ISO) and organize to support direct implementation in the compiler (one downside is not getting to go to Hawaii).
The future of compiler development is groups of like-minded hedonists (in the sense of agreeing what features should be in a language) supporting a compiler for the bragging rights of having created/designed the languages features used by hundreds of thousands of developers.
Early compiler history
Who wrote the early compilers, when did they do it and what were the languages compiled?
Answering these questions requires defining what we mean by ‘compiler’ and deciding what counts as a language.
Donald Knuth does a masterful job of covering the early development of programming languages. People were writing programs in high level languages well before the 1950s and Konrad Zuse is the forgotten pioneer from the 1940s (it did not help that Germany had just lost a war and people were not inclined to given German’s much public credit).
What is the distinction between a compiler and an assembler? Some early ‘high-level’ languages look distinctly low-level from our much later perspective; some assemblers support fancy subroutine and macro facilities that give them a high-level feel.
Glennie’s Autocode is from 1952 and depending on where the compiler/assembler line is drawn might be considered a contender for the first compiler. The team led by Grace Hopper produced A-0, a fancy link-loaded, in 1952; they called it a compiler, but today we would not consider it to be one.
Talking of Grace Hopper, from a biography of her technical contributions she sounds like a person who could be technical but chose to be management.
Fortran and Cobol hog the limelight of early compiler history.
Work on the first Fortran compiler started in the summer of 1954 and was completed 2.5 years later, say the beginning of 1957. A very solid claim to being the first compiler (assuming Autocode and A-0 are not considered to be compilers).
Compilers were created for Algol 58 in 1958 (a long dead language implemented in Germany with the war still fresh in people’s minds; not a recipe for wide publicity) and 1960 (perhaps the first one-man-band implemented compiler; written by Knuth, an American, but still a long dead language). The 1958 implementation sounds like it has a good claim to being the second compiler after the Fortran compiler.
In December 1960 there were at least two Cobol compilers in existence (one of which was created by a team containing Grace Hopper in a management capacity). I think the glory attached to early Cobol compiler work is the result of having a female lead involved in the development team of one of these compilers. Why isn’t the other Cobol compiler ever mentioned? Why is the Algol 58 compiler implementation that occurred before the Cobol compiler ever mentioned?
What were the early books on compiler writing?
“Algol 60 Implementation” by Russell and Randell (from 1964) still appears surprisingly modern.
Principles of Compiler Design, the “Dragon book”, came out in 1977 and was about the only easily obtainable compiler book for many years. The first half dealt with the theory of parser generators (the audience was CS undergraduates and parser generation used to be a very trendy topic with umpteen PhD thesis written about it); the book morphed into Compilers: Principles, Techniques, and Tools. Old-timers will reminisce about how their copy of the book has a green dragon on the front, rather than the red dragon on later trendier (with less parser theory and more code generation) editions.
Happy 30th birthday to GCC
Thirty years ago today Richard Stallman announced the availability of a beta version of gcc on the mod.compilers newsgroup.
Everybody and his dog was writing C compilers in the late 1980s and early 1990s (a C compiler validation suite vendor once told me they had sold over 150 copies; a compiler vendor has to be serious to fork out around $10,000 for a validation suite). Did gcc become the dominant open source because one compiler would inevitably become dominant, or was there some collection of factors that gave gcc a significant advantage?
I think gcc’s market dominance was driven by two environmental factors, with some help from a technical compiler implementation decision.
The technical implementation decision was the use of RTL as the optimization+code generation strategy. Jack Davidson’s 1981 PhD thesis (and much later the LCC book) describe the gory details. The code generators for nearly every other C compiler was closely tied to the machine being targeted (because the implementers were focused on getting a job done, not producing a portable compiler system). Had they been so inclined Davidson and Christopher Fraser could have been the authors of the dominant C compiler.
The first environment factor was the creation of a support ecosystem around gcc. The glue that nourished this ecosystem was the money made writing code generators for the never ending supply of new cpus that companies were creating (that needed a C compiler). In the beginning Cygnus Solutions were the face of gcc+tools; Michael Tiemann, a bright affable young guy, once told me that he could not figure out why companies were throwing money at them and that perhaps it was because he was so tall. Richard Stallman was not the easiest person to get along with and was probably somebody you would try to avoid meeting (I don’t know if he has mellowed). If Cygnus had gone with a different compiler, they had created 175 host/target combinations by 1999, gcc would be as well-known today as Hurd.
Yes, people writing Masters and PhD thesis were using gcc as the scaffolding for their fancy new optimization techniques (e.g., here, here and here), but this work essentially played the role of an R&D group trying to figure out where effort ought to be invested writing production code.
Sun’s decision to unbundle the development environment (i.e., stop shipping a C compiler with every system) caused some developers to switch to another compiler, some choosing gcc.
The second environment factor was the huge leap in available memory on developer machines in the 1990s. Compiler vendors cannot ship compilers that do fancy optimization if developers don’t have computers with enough memory to hold the optimization information (many, many megabytes). Until developer machines contained lots of memory, a one-man band could build a compiler producing code that was essentially as good as everybody else. An open source market leader could not emerge until the man+dog compilers could be clearly seen to be inferior.
During the 1990s the amount of memory likely to be available in developers’ computers grew dramatically, allowing gcc to support more and more optimizations (donated by a myriad of people targeting some aspect of code generation that they found interesting). Code generation improved dramatically and man+dog compilers became obviously second/third rate.
Would things be different today if Linus Torvalds’ had not selected gcc? If Linus had chosen a compiler licensed under a more liberal license than copyleft, things might have turned out very differently. LLVM started life in 2003 and one of my predictions for 2009 was its demise in the next few years; I failed to see the importance of licensing to Apple (who essentially funded its development).
Eventually, success.
With success came new existential threats, in particular death by a thousand forks.
A serious fork occurred in 1997. Stallman was clogging up the works; fortunately he saw the writing on the wall and in 1999 stepped aside.
Money is what holds together the major development teams supporting gcc and llvm. What happens when customers wanting support for new back-ends dries up, what happens when major companies stop funding development? Do we start seeing adverts during compilation? Chris Lattner, the driving force behind llvm recently moved to Tesla; will it turn out that his continuing management was as integral to the continuing success of llvm as getting rid of Stallman was to the continuing success of gcc?
Will a single mainline version of gcc still be the dominant compiler in another 30 years time?
Time will tell.
C compilers of the 20th century running on Microsoft operating systems
There used to be a huge variety of C compilers available for sale under MS-DOS and later Microsoft Windows. A C compiler validation suite vendor once told me they had sold over 150 copies; a compiler vendor has to be serious to fork out around $10,000 for a validation suite (actually good value for money given the volume of tests in a commercial suite).
C compilers of the 20th century running on Microsoft operating systems would make a great specialist subject for a Mastermind contestant. The August 1983 issue of BYTE must be the go-to reference for C in the 1980s.
Here is my current list of compilers that were once and perhaps still are commercially available on Microsoft operating systems.
Aztec C: from Manx Software Systems.
Borland C: from Borland
IBM PC C Compiler: from Lattice???
CI-C86: from Computer Innovations.
CSI-C:…
DeSmet C:…
Digital Research C: Was this ever sold on a Microsoft OS?
Eco-C and Eco-C88 C:…
LCC: sold as a book in the 20th century, but its Microsoft OS implementations, such as lcc-win (with over 2 million copies distributed) and Pelles C, are really 21st century compilers.
Mark Williams C compiler: A US company having an entry in the German Wikipedia ranked significantly higher by Google than its English Wikipedia page shows that this compiler was a big success on the Atari ST (very popular in Germany) but not DOS/Windows.
Microsoft C: The compiler that nobody got fired for buying. Vendors had to try hard generate worse code than this compiler (which some achieved, i.e., MIX) and also very hard to provide better the runtime support (which nobody ever could). Version 2 of Microsoft C was actually the Lattice C compiler.
MIX C from Mix Software
NDP C:…
Supersoft C:…
TopSpeed C: from Jensen & Partners International.
Watcom C: open sourced as Open Watcom
Wizard C: from Bob Jervis who sold (licensed???) it to Borland, where it became Turbo C.
Zorland C, Zortech C: from Walter Bright and my compiler of choice for several years.
If you know of a compiler that is missing from this list, or have better information, please let me know in the comments. Hopefully I will start to remember more about long forgotten C compilers.
cpu+FPGA: applications can soon have bespoke instructions
Compiler writers are always frustrated that the cpu they are currently targeting does not contain the one instruction that would enable them to generate really efficient code. If only it were possible to add new instructions to the cpu. Well, it looks like this will soon be possible; Intel have added an on chip FPGA to their Broadwell processor (available circa 2017).
Having custom instructions on a FPGA (they would be loaded at program startup) is not the same as having the instructions on the cpu itself, there will be communication overhead when the data operated on by the custom instruction get transferred back and forth between cpu/FPGA (being on-chip means this will be low). To make the exercise worthwhile the custom instruction has to do something that takes very many cycles on the cpu and either speeds it up or reduces the power consumed (the Catapult project at Microsoft has a rack of FPGA enhanced machines speeding up/reducing the power of matching search engine queries to documents).
A CPU+FPGA is like CPU+GPU, except that FPGAs are programmed at a much lower level, i.e., there is little in the way of abstraction between what the hardware does and what the coder sees.
Does the world need a FPGA attached to their cpu? Most don’t but there are probably a few customers who do, e.g., data centers with systems performing dedicated tasks and anybody into serious bit twiddling. Other considerations include Intel needing to add new bells and whistles to its product so that customers who have been trained over the years to buy the very latest product (which has the largest margins) stay on the buying treadmill. The FPGA is also a differentiator, not that Intel would ever think of AMD as a serious competitor.
Initially the obvious use case is libraries performing commonly occurring functionality. No, not matrix multiple and inverse, FPGA are predominantly integer operation units (there are approaches using non-standard floating-point formats that can be used if your FPGA unit does not have floating-point support).
From the compiler perspective the use case is spotting cpu intensive loops, where all the data can be held on the FPGA until processing is complete. Will there be enough of these loops to make it a worthwhile implementation target? I suspect not. But then I can see many PhDs being written on this topic and one of them could produce a viable implementation that bootstraps itself into one of the popular open source compilers.
Interpreters have to do a lot of housekeeping work. Perhaps programs written in Java or R could be executed on the FPGA that uses the cpu as a slave processor. It is claimed that most R programs spend their time in library functions that have been implemented in C and Fortran, but I’m seeing more and more code that appears to be all R. For some programs an R-machine implemented in hardware could produce orders of magnitude speed improvements.
The next generation of cryptocurrency proof-of-work algorithms are being designed to be memory intensive, so they cannot be efficiently implemented using ASIC-proof (this prevents mining being concentrated in a few groups who have built bespoke mining operations). The analysis I have seen is based on ‘conventional’ cpu and ASIC designs. A cpu+FPGA is a very different kind of beast and one that might require another round of cryptocurrency design.
These cpu+FPGA processors have the potential to dramatically upend existing approaches to structuring programs. Very interesting times ahead!
Recent Comments