Archive
Forces driving patterns found in call graphs of human written code
It has been a while since I posted anything about generating source that mimics the characteristics of human written code.
Generating function definitions is the easy bit, although variable selection is fiddly and naming needs to be handled.
The hardest part of mimicking human written code is linking functions together, via calls, in apparently meaningful ways. Within one source file it is probably possible to get away with individual calls to other local functions (most function definitions are called once) and a couple of calls to third party libraries. At the complete program level the code needs to tell a story, and doing this is very hard.
I think function calls can be divided into three categories, all based on the relationship between the developer who writes the code than does the call and the developer(s) who wrote the called function:
- Caller developer is the same person as the callee developer. One person gets to decide how things are done,
- Caller developer works on the same team as the callee developer. Here an interface needs to be negotiated with one or more other people,
- Caller developer is making use of a third-party library. The interface is pre-decided, take it or leave it (the same principle applies to library updates, the caller has to decide whether to stay with the existing version or make the changes needed to upgrade to the new version; Android is the (in)famous example of a frequently changed library that developers are under strong pressure to continually adapt to).
Calls to functions in third-party libraries tend to follow stylized sequences, e.g., open_* occurs before read_*/write_* and close_* appears last. Most of the time a generator could get away not calling functions from third-party libraries, because the number of such calls is often small, but when they occur they had better look correct.
Needing to call a function written by another developer on the team opens up all sorts of possibilities: there is always the option of them modifying the function to make life easier for the new call, but the cost of modifying all the existing call sites (plus any associated call chains) may be too high, perhaps a new global variable can be used to communicate the desired information, or perhaps the proposed usage is a small cog in a large wheel and has to make do (or perhaps they don’t like the person asking for the change and reasons are invented for staying as-is).
Then there is correlation in time and space (this has a big impact on patterns of evolution, at least I think so; models of forest fires, i.e., growth, death, fires of various sizes creating space for new growth, is the obvious parallel):
- The longer a function exists the more likely it is to accumulate callers. A function definition can remain unchanged and yet over time become more and more difficult to change.
- It can be very expensive to make changes to an existing function definition when there are lots of calls to it.
What do measurements of code have to say? Almost nothing; existing studies mostly do weird things like treating a system’s call graph as-if it were a social network (using a currently trendy metaphor is good for getting papers published, even if the mapping is all wrong), plotting power law-like graphs and sprouting portentous nonsense.
What is really needed is measurements of forked systems; comparing systems derived from a common past will tell us how much natural variation exists due to individual choice.
FreeBSD, NetBSD and OpenBSD are the obvious poster children of forked, common heritage, systems written in C; I cannot think of any such systems written in Java or C++.
Wot, apply academic work in industry?
Academics often moan about industry not making use of their work (or at least they do within the code analysis niche I frequent, I have no real knowledge of other niches). There are three reasons for this state of affairs:
- The work that most academics do has no practical relevance to industry. This is the lion’s share of the reason and something that many academics will agree with if none of their colleges are likely to overhear them. I suspect many academics are not too fussed that their work is not used by industry and are happy to continue working on things they find interesting (or that they can write papers about that disconnected souls are happy to see published).
- Very very few people in the software industry ever read academic papers. But hey, not reading manuals is regarded as a badge of honour. Some people do read manuals and are quickly elevated to expert status. Academic papers do have a very low signal to noise ratio and learning to speed read them to locate the gold nuggets takes practice.
- If an academic’s work is applied by some company the last thing those involved will do is say anything about it. Industry is a cut-throat place and what is to be gained by freely giving useful information to the competition?
The second product my company ever produced was a range of code generators for an intermediate code that was currently interpreted; how best to match the patterns in the intermediate code and also reuse as much as possible for the different cpu targets? I found a solution in Mahadevan Ganapahi’s PhD thesis and now 33 years after publishing it he gets some credit for a long gone industrial application.
Compiler benchmarking for the 21st century
I would like to propose a new way of measuring the quality of a compiler’s code generator: The highest quality compiler is one that generates identical code for all programs that produce the same output, e.g., a compiler might spot programs that calculate pi and always generate code that uses the most rapidly converging method known. This is a very different approach to the traditional methods based on using (mostly) execution time or size (usually code but sometimes data) as a measure of quality.
Why is a new measurement method needed and why choose this one? It is relatively easy for compiler vendors to tune their products to the commonly used benchmark and they seem to have lost their role as drivers for new optimization techniques. Different developers have different writing habits and companies should not have to waste time and money changing developer habits just to get the best quality code out of a compiler; compilers should handle differences in developer coding habits and not let it affect the quality of generated code. There are major savings to be had by optimizing the effect that developers are trying to achieve rather than what they have actually written (these days new optimizations targeting at what developers have written show very low percentage improvements).
Deducing that a function calculates pi requires a level of sophistication in whole program analysis that is unlikely to be available in production compilers for some years to come (ok, detecting 4*atan(1.0) is possible today). What is needed is a collection of compilable files containing source code that aims to achieve an outcome in lots of different ways. To get the ball rolling the “3n times 2” problem is presented as the first of this new breed of benchmarks.
The “3n times 2” problem is a variant on the 3n+1 problem that has been tweaked to create more optimization opportunities. One implementation of the “3n times 2” problem is:
if (is_odd(n)) n = 3*n+1; else n = 2*n; // this is n = n / 2; in the 3n+1 problem |
There are lots of ways of writing code that has the same effect, some of the statements I have seen for calculating n=3*n+1 include: n = n + n + n + 1, n = (n << 1) + n + 1 and n *= 3; n++, while some of the ways of checking if n is odd include: n & 1, (n / 2)*2 != n and n % 2.
I have created a list of different ways in which 3*n+1 might be calculated and is_odd(n) might be tested and written a script to generate a function containing all possible permutations (to reduce the number of combinations no variants were created for the least interesting case of n=2*n, which was always generated in this form). The following is a snippet of the generated code (download everything):
if (n & 1) n=(n << 2) - n +1; else n*=2; if (n & 1) n=3*n+1; else n*=2; if (n & 1) n += 2*n +1; else n*=2; if ((n / 2)*2 != n) { t=(n << 1); n=t+n+1; } else n*=2; if ((n / 2)*2 != n) { n*=3; n++; } else n*=2; |
Benchmarks need a means of summarizing the results and here I make a stab at doing that for gcc 4.6.1 and llvm 2.9, when executed using the -O3 option (output here and here). Both compilers generated a total of four different sequences for the 27 'different' statements (I'm not sure what to do about the inline function tests and have ignored them here) with none of the sequences being shared between compilers. The following lists the number of occurrences of each sequence, e.g., gcc generated one sequence 16 times, another 8 times and so on:
gcc 16 8 2 1 llvm 12 6 6 3
How might we turn these counts into a single number that enables compiler performance to be compared? One possibility is to award 1 point for each of the most common sequence, 1/2 point for each of the second most common, 1/4 for the third and so on. Using this scheme gcc gets 20.625, and llvm gets 16.875. So gcc has greater consistency (I am loathed to use the much over used phrase higher quality).
Now for a closer look at the code generated.
Both compilers always generated code to test the least significant bit for the conditional expressions n & 1 and n % 2. For the test (n / 2)*2 != n gcc generated the not very clever right-shift/left-shift/compare while llvm and'ed out the bottom bit and then compared; so both compilers failed to handle what is a surprisingly common check for a number being odd.
The optimal code for n=3*n+1 on a modern x86 processor is (lots of register combinations are possible, lets assume rdx contains n) leal 1(%rdx,%rdx,2), %edx and this is what both compilers generated a lot of the time. This locally optimal code is not always generated because:
- gcc fails to detect that
(n << 2)-n+1is equivalent to(n << 1)+n+1and generates the sequenceleal 0(,%rax,4), %edx ; subl %eax, %edx ; addl $1, %edx(I pointed this out to a gcc maintainer sometime ago and he suggested reporting it as a bug). This 'bug' occurs occurs three times in total. - For some forms of the calculation llvm generates globally better code by taking the else arm into consideration. For instance, when the calculation is written as
n += (n << 1) +1llvm deduces that(n << 1)and the2*nin theelseare equivalent, evaluates this value into a register before performing the conditional test thus removing the need for an unconditional jump around the 'else' code:leal (%rax,%rax), %ecx testb $1, %al je .LBB0_8 # BB#7: orl $1, %ecx # deduced ecx is even, arithmetic unit not needed! addl %eax, %ecx .LBB0_8:
This more efficient sequence occurs nine times in total.
The most optimal sequence was generated by gcc:
testb $1, %dl leal (%rdx,%rdx), %eax je .L6 leal 1(%rdx,%rdx,2), %eax .L6: |
with llvm and pre 4.6 versions of gcc generating the more traditional form (above, gcc 4.6.1 assumes that the 'then' arm is the most likely to be executed and trades off a leal against a very slow jmp):
testb $1, %al je .LBB0_5 # BB#4: leal 1(%rax,%rax,2), %eax jmp .LBB0_6 .LBB0_5: addl %eax, %eax .LBB0_6: |
There is still room for improvement, perhaps by using the conditional move instruction (which gcc actually generates within the not-very-clever code sequence for (n / 2)*2 != n) or by using the fact that eax already holds 2*n (the potential saving would come through a reduction in complexity of the internal resources needed to execute the instruction).
llvm insists on storing the calculated value back into n at the end of every statement. I'm not sure if this is a bug or a feature designed to make runtime debugging easier (if so it ought to be switched off by default).
Missed optimization opportunities (not intended to be part of this benchmark and if encountered would require a restructuring of the test source) include noticing that if  is odd then
is odd then 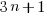 is always even, creating the opportunity to perform the following multiply by 2 without an if test.
is always even, creating the opportunity to perform the following multiply by 2 without an if test.
Perhaps one days compilers will figure out when a program is calculating pi and generate code that uses the best known algorithm. In the meantime I am interested in hearing suggestions for additional different-algorithm-same-code benchmarks.
Simple generator for compiler stress testing source
Since writing my C book I have been interested in the problem of generating source that has the syntactic and semantic statistical characteristics of human written code.
Generating code that obeys a language’s syntax is straight forward. Take a specification of the syntax (say is some yacc-like form) and ‘generate’ each of the terminals/nonterminals on the right-hand-side of the start symbol. Nonterminals will lead to rules having right-hand-sides that in turn need to be ‘generated’, a random selection being made when a nonterminal has more than one possible rhs rule. Output occurs when a terminal is ‘generated’.
For the code to mimic human written code it is necessary to bias the random selection process; a numeric value at the start of each rhs rule can be used to specify the percentage probability of that rule being chosen for the corresponding nonterminal.
The following example generates a subset of C expressions; nonterminals in lowercase, terminals in uppercase and implemented as a call to a function having that name:
%grammar first_rule : def_ident " = " expr " ;\n" END_EXPR_STMT ; def_ident : MK_IDENT ; constant : MK_CONSTANT ; identifier : KNOWN_IDENT ; primary_expr : 30 constant | 60 identifier | 10 " (" expr ") " ; multiplicative_expr : 50 primary_expr | 40 multiplicative_expr " * " primary_expr | 10 multiplicative_expr " / " primary_expr ; additive_expr : 50 multiplicative_expr | 25 additive_expr " + " multiplicative_expr | 25 additive_expr " - " multiplicative_expr ; expr : START_EXPR additive_expr FINISH_EXPR ; |
A 250 line awk program (awk only because I use it often enough for simply text processing that it is second nature) translates this into two Python lists:
productions = [ [0], [ 1, 1, 1, # first_rule 0, 5, [2, 1001, 3, 1002, 1003, ], ], [ 2, 1, 1, # def_ident 0, 1, [1004, ], ], [ 4, 1, 1, # constant 0, 1, [1005, ], ], [ 5, 1, 1, # identifier 0, 1, [1006, ], ], [ 6, 3, 0, # primary_expr 30, 1, [4, ], 60, 1, [5, ], 10, 3, [1007, 3, 1008, ], ], [ 7, 3, 0, # multiplicative_expr 50, 1, [6, ], 40, 3, [7, 1009, 6, ], 10, 3, [7, 1010, 6, ], ], [ 8, 3, 0, # additive_expr 50, 1, [7, ], 25, 3, [8, 1011, 7, ], 25, 3, [8, 1012, 7, ], ], [ 3, 1, 1, # expr 0, 3, [1013, 8, 1014, ], ], ] terminal = [ [0], [ STR_TERM, " = "], [ STR_TERM, " ;\n"], [ FUNC_TERM, END_EXPR_STMT], [ FUNC_TERM, MK_IDENT], [ FUNC_TERM, MK_CONSTANT], [ FUNC_TERM, KNOWN_IDENT], [ STR_TERM, " ("], [ STR_TERM, ") "], [ STR_TERM, " * "], [ STR_TERM, " / "], [ STR_TERM, " + "], [ STR_TERM, " - "], [ FUNC_TERM, START_EXPR], [ FUNC_TERM, FINISH_EXPR], ] |
which can be executed by a simply interpreter:
def exec_rule(some_rule) : rule_len=len(some_rule) cur_action=0 while (cur_action < rule_len) : if (some_rule[cur_action] > term_start_base) : gen_terminal(some_rule[cur_action]-term_start_base) else : exec_rule(select_rule(productions[some_rule[cur_action]])) cur_action+=1 productions.sort() start_code() ns=0 while (ns < 2000) : # Loop generating lots of test cases exec_rule(select_rule(productions[1])) ns+=1 end_code() |
Naive syntax-directed generation results in a lot of code that violates one or more fundamental semantic constraints. For instance the assignment (1+1)=3 is syntactically valid in many languages, which invariably specify a semantic constraint on the lhs of an assignment operator being some kind of modifiable storage location. The simplest solution to this problem is to change the syntax to limit the kinds of constructs that can be generated on the lhs of an assignment.
The hardest semantic association to get right is the connection between variable declarations and references to those variables in expressions. One solution is to mimic how I think many developers write code, that is to generate the statements first and then generate the required definitions for the appropriate variables.
A whole host of minor semantic issues require the syntax generated code to be tweaked, e.g., division by zero occurs more often in untweaked generated code than human code. There are also statistical patterns within the semantics of human written code, e.g., frequency of use of local variables, that need to be addressed.
A few weeks ago the source of Csmith, a C source generator designed to stress the code generation phase of a compiler, was released. Over the years various people have written C compiler stress testers, most recently NPL implemented one in Java, but this is the first time that the source has been released. Imagine my disappointment on discovering that Csmith contained around 40 KLOC of code, only a bit smaller than a C compiler I had once help write. I decided to see if my ‘human characteristics’ generator could be used to create a compiler code generator stress tester.
The idea behind compiler code generator stress testing is to generate a program containing some complicated sequence of code, compile and run it, comparing the value produced against the value that is supposed to be produced.
I modified the human characteristics generator to produce pairs of statements like the following:
i = i_3 * i_6 & i_2 << i_7 ; chk_result(i, 3 * 6 & 2 << 7, __LINE__); |
the second argument to chk_result is the value that i should contain (while generating the expression to assign to i the corresponding constant expression with the variables replaced by their known values is also created).
Having the compiler evaluate the constant expression simplifies the stress tester and provides another check that the compiler gets things right (or gets two different things wrong in the same way, in which case we probably don’t get to see any failure message). The first gcc bug I found concerned this constant expression (in fact this same compiler bug crops up with alarming regularity in the generated code).
As previously mentioned connecting variables in expressions to a corresponding definition is a lot of work. I simplified this problem by assuming that an integer variable i would be predefined in the surrounding support code and that this would be the only variable ever assigned to in the generated code.
There is some simple house-keeping that wraps everything within a program and provides the appropriate variable definitions.
The grammar used to generate full C expressions is 228 lines, the awk translator 252 lines and the Python interpreter 55 lines; just over 1% of Csmith in LOC and it is very easy to configure. However, an awful lot functionality needs to be added before it starts to rival Csmith, not least of which is support for assignment to more than one integer variable!
Recent Comments