Archive
Relative performance of computers from the 1950s/60s/70s
What was the range of performance of computers introduced in the 1950, 1960s and 1970s, and what was the annual rate of increase?
People have been measuring computer performance since they were first created, and thanks to the Internet Archive the published results are sometimes available today. The catch is that performance was often measured using different benchmarks. Fortunately, a few benchmarks were run on many systems, and in a few cases different benchmarks were run on the same system.
I have found published data on four distinct system performance estimation models, with each applied to 100+ systems (a total of 1,306 systems, of which 1,111 are unique). There is around a 20% overlap between systems across pairs of models, i.e., multiple models applied to the same system. The plot below shows the reported performance for pairs of estimates for the same system (code+data):
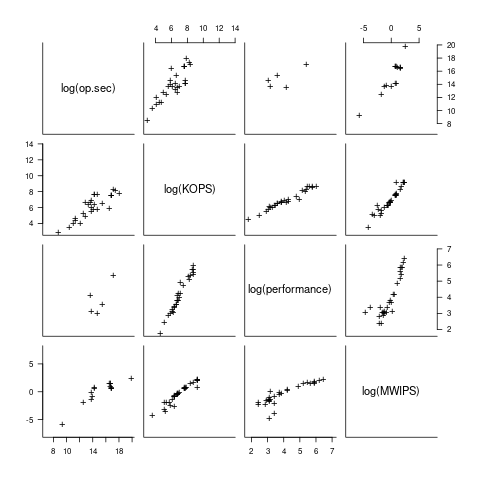
The relative performance relationship between pairs of different estimation models for the same system is linear (on a log scale).
Each of the models aims to produce a result that is representative of typical programs, i.e., be of use to people trying to decide which system to buy.
- Kenneth Knight built a structural model, based on 30 or so system characteristics, such as time to perform various arithmetic operations and I/O time; plugging in the values for a system produced a performance estimate. These characteristics were weighted based on measurements of scientific and commercial applications, to calculate a value that was representative of scientific or commercial operation. The Knight data appears in two magazine articles analysing systems from the 1950s and 1960s (the 310 rows are discussed in an earlier post), and the 1985 paper “A functional and structural measurement of technology”, containing data from the late 1960s and 1970s (120 rows),
- Ein-Dor and Feldmesser also built a structural model, based on the characteristics of 209 systems introduced between 1981 and 1984,
- The November 1980 Datamation article by Edward Lias lists what he called the KOPS (thousands of operations per second, i.e., MIPS for slower systems) value for 237 systems. Similar to the Knight and Ein-dor data, the calculated value is based on weighting various cpu instruction timings
- The Whetstone benchmark is based on running a particular program on a system, and recording its performance; this benchmark was designed to be representative of scientific and engineering applications, i.e., floating-point intensive. The design of this benchmark was the subject of last week’s post. I extracted 504 results from Roy Longbottom’s extensive collection of Whetstone results going back to the mid-1960s.
While the Whetstone benchmark was originally designed as an Algol 60 program that was representative of scientific applications written in Algol, only 5% of the results used this version of the benchmark; 85% of the results used the Fortran version. Fitting a regression model to the data finds that the Fortran version produced higher results than the Algol 60 version (which would encourage vendors to use the Fortran version). To ensure consistency of the Whetstone results, only those using the Fortran benchmark are used in this analysis.
A fifth dataset is the Dhrystone benchmark followed in the footsteps of the Whetstone benchmark, but targetting integer-based applications, i.e., no floating-point. First published in 1984, most of the Dhrystone results apply to more recent systems than the other benchmarks. This code+data contains the 328 results listed by the Performance Database Server.
Sometimes slightly different system names appear in the published results. I used the system names appearing in the Computers Models Database as the definitive names. It is possible that a few misspelled system names remain in the data (the possible impact is not matching systems up across models), please let me know if you spot any.
What is the best statistical technique to use to aggregate results from multiple models into a single relative performance value?
I came up with various possibilities, none of which looked that good, and even posted a question on Cross Validated (no replies yet).
Asking on the Evidence-based software engineering Discord channel produced a helpful reply from Neal Fultz, i.e., use the random effects model: lmer(log(metric) ~ (1|System)+(1|Bench), data=Sall_clean) ; after trying lots of other more complicated approaches, I would probably have eventually gotten around to using this approach.
Does this random effects model produce reliable values?
I don’t have a good idea how to evaluate the fitted model. Looking at pairs of systems where I know which is faster, the relative model values are consistent with what I know.
A csv of the calculated system relative performance values. I have yet to find a reliable way of estimating confidence bounds on these values.
The plot below shows the performance of systems introduced in a given year, on a relative scale, red line is a fitted exponential model (a factor of 5.5 faster, annually; code+data):
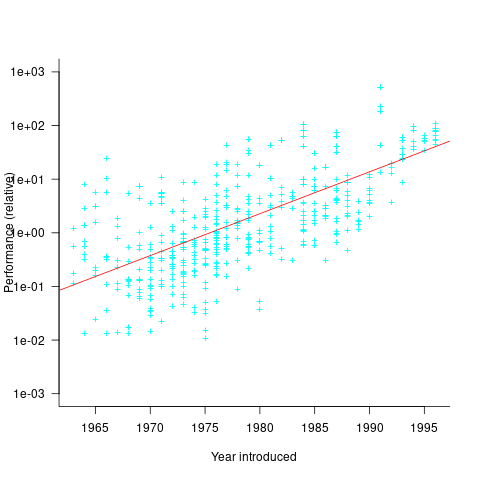
If you know of a more effective way of analysing this data, or any other published data on system benchmarks for these decades, please let me know.
Design of the Whetstone benchmark
The Whetstone benchmark was once a widely cited measure of computer performance. This benchmark consisted of a single program, originally designed for Algol 60 based applications, and later translated to other languages (over 85% of published results used Fortran). The source used as representative of typical user programs came from scientific applications, which has some characteristics that are very non-representative of non-scientific applications, e.g., use of floating-point, and proportionally more multiplications and multidimensional array accesses. Dhrystone benchmark was later designed with the intent of being representative of a broader range of applications.
While rooting around for Whetstone result data, I discovered the book Algol 60 Compilation and Assessment by Brian Wichmann. Despite knowing Brian for 25 years and being very familiar with his work on compiler validation, I had never heard of this book (Knuth’s An Empirical Study of Fortran Programs has sucked up all the oxygen in this niche).
As expected, this 1973 book has a very 1960s model of cpu/compiler behavior, much the same as MIX, the idealised computer used by Knuth for the first 30-years of The Art of Computer Programming.
The Whetstone world view is of a WYSIWYG compiler (i.e., each source statement maps to the obvious machine code), and cpu instructions that always take the same number of clock cycles to execute (the cpu/memory performance ratio had not yet moved far from unity, for many machines).
Compiler optimization is all about trying not to generate code, and special casing to eke out many small savings; post-1970 compilers tried hard not to be WYSIWYG. Showing compiler correctness is much simplified by WYSIWIG code generation.
Today, there are application domains where the 1960s machine model still holds. Low power embedded systems may have cpu/memory performance ratios close to unity, and predictable instruction execution times (estimating worst-case execution time is a minor research field).
Creating a representative usage-based benchmark requires detailed runtime data on what the chosen representative programs are doing. Brian modified the Whetstone Algol interpreter to count how many times each virtual machine op-code was executed (see the report Some Statistics from ALGOL Programs for more information).
The modified Algol interpreter was installed on the KDF9 at the National Physical Laboratory and Oxford University, in the late 1960s. Data from 949 programs was collected; the average number of operations per program was 152,000.
The op-codes need to be mapped to Algol statements, to create a benchmark program whose compiled form executes the appropriate proportion of op-codes. Some op-code sequences map directly to statements, e.g., Ld addrof x, Ld value y, Store, maps to the statement: x:=y;.
Counts of occurrences of each language construct in the source of the representative programs provides lots of information about the proportions of the basic building blocks. It’s ‘just’ a matter of sorting out the loop counts.
For me, the most interesting part of the book is chapter 2, which attempts to measure the execution time of 40+ different statements running on 36 different machines. The timing model is 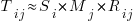 , where
, where 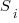 is the
is the 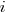 ‘th statement,
‘th statement, 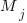 is the
is the 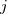 ‘th machine,
‘th machine, 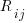 an adjustment factor intended to be as close to one as possible, and
an adjustment factor intended to be as close to one as possible, and 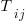 is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
is execution time. The book lists some of the practical issues with this model, from the analysis of timing data from current machines, e.g., the impact of different compilers, and particular architecture features having a big performance impact on some kinds of statements.
The table below shows statement execution time, in microseconds, for the corresponding computer and statement (* indicates an estimate; the book contains timings on 36 systems):
ATLAS MU5 1906A RRE Algol 68 B5500 Statement 6.0 0.52 1.4 14.0 12.1 x:=1.0 6.0 0.52 1.3 54.0 8.1 x:=1 6.0 0.52 1.4 *12.6 11.6 x:=y 9.0 0.62 2.0 23.0 18.8 x:=y + z 12.0 0.82 3.2 39.0 50.0 x:=y × z 18.0 2.02 7.2 71.0 32.5 x:=y/z 9.0 0.52 1.0 8.0 8.1 k:=1 18.0 0.52 0.9 121.0 25.0 k:=1.0 12.0 0.62 2.5 13.0 18.8 k:=l + m 15.0 1.07 4.9 75.0 35.0 k:=l × m 48.0 1.66 6.7 45.0 34.6 k:=l ÷ m 9.0 0.52 1.9 8.0 11.6 k:=l 6.0 0.72 3.1 44.0 11.8 x:=l 18.0 0.72 8.0 122.0 26.1 l:=y 39.0 0.82 20.3 180.0 46.6 x:=y ^ 2 48.0 1.12 23.0 213.0 85.0 x:=y ^ 3 120.0 10.60 55.0 978.0 1760.0 x:=y ^ z 21.0 0.72 1.8 22.0 24.0 e1[1]:=1 27.0 1.37 1.9 54.0 42.8 e1[1, 1]:=1 33.0 2.02 1.9 106.0 66.6 e1[1, 1, 1]:=1 15.0 0.72 2.4 22.0 23.5 l:=e1[1] 45.0 1.74 0.4 52.0 22.3 begin real a; end 96.0 2.14 80.0 242.0 2870.0 begin array a[1:1]; end 96.0 2.14 86.0 232.0 2870.0 begin array a[1:500]; end 156.0 2.96 106.0 352.0 8430.0 begin array a[1:1, 1:1]; end 216.0 3.46 124.0 452.0 13000.0 begin array a[1:1, 1:1, 1:1]; end 42.0 1.56 3.5 16.0 31.5 begin goto abcd; abcd : end 129.0 2.08 9.4 62.0 98.3 begin switch s:=q; goto s[1]; q : end 210.0 24.60 73.0 692.0 598.0 x:=sin(y) 222.0 25.00 73.0 462.0 758.0 x:=cos(y) 84.0 *0.58 17.3 22.0 14.0 x:=abs(y) 270.0 *10.20 71.0 562.0 740.0 x:=exp(y) 261.0 *7.30 24.7 462.0 808.0 x:=ln(y) 246.0 *6.77 73.0 432.0 605.0 x:=sqrt(y) 272.0 *12.90 91.0 622.0 841.0 x:=arctan(y) 99.0 *1.38 18.7 72.0 37.5 x:=sign(y) 99.0 *2.70 24.7 152.0 41.1 x:=entier(y) 54.0 2.18 43.0 72.0 31.0 p0 69.0 *6.61 57.0 92.0 39.0 p1(x) 75.0 *8.28 65.0 132.0 45.0 p2(x, y) 93.0 *9.75 71.0 162.0 53.0 p2(x, y, z) 57.0 *0.92 8.6 17.0 38.5 loop time |
The performance studies found wide disparities between expected and observed timings. Chapter 9 does a deep dive on six Algol compilers.
A lot of work and idealism went into gather the data for this book (36 systems!). Unfortunately, the computer performance model was already noticeably inaccurate, and advances in compiler optimization and cpu design meant that the accuracy was only going to get worse. Anyways, there is lots of interesting performance data on 1960 era computers.
Whetstone lived on into the 1990s, when the SPEC benchmark started to its rise to benchmark dominance.
Benchmarking fuzzers
Fuzzing has become a popular area of research in the reliability & testing community, with a stream of papers claiming to have created a better tool/algorithm. The claims of ‘betterness’, made by the authors, often derive from the number of previously unreported faults discovered in some collection of widely used programs.
Developers in industry will be interested in using fuzzing if it provides a cost-effective means of discovering coding mistakes that are likely to result in customers experiencing a serious fault. This requirement roughly translates to: minimal cost for finding maximal distinct mistakes (finding the same mistake more than once is wasted effort); whether a particular coding mistake is likely to produce a serious customer fault is a decision decided by people.
How do different fuzzing tools compare, when benchmarking the number of distinct mistakes they each find, for a given amount of cpu time?
TL;DR: I don’t know, and this approach is probably not a useful way of comparing fuzzers.
Fuzzing researchers are currently competing on the number of previously unreported faults discovered, i.e., not listed in the fuzzed program’s database of fault reports. Most research papers only report the number of distinct faults discovered in each program fuzzed, the amount of wall clock hours/days used (sometimes weeks), and the characteristics of the computer/cluster on which the campaign was run. This may be enough information to estimate an upper bound on faults per unit of cpu time; more detailed data is rarely available (I have emailed the authors of around a dozen papers asking for more detailed data).
A benchmark based on comparing faults discovered per unit of cpu time only makes sense when the new fault discovery rate is roughly constant. Experience shows that discovery time can vary by orders of magnitude.
Code coverage is a fuzzer performance metric that is starting to be widely used by researchers. Measures of coverage include: statements/basic blocks, conditions, or some object code metric. Coverage has the advantage of providing defined fuzzer objectives (e.g., generate input that causes uncovered code to be executed), and is independent of the number of coding mistakes present in the code.
How is a fuzzer likely to be used in industry?
The fuzzing process may be incremental, discovering a few coding mistakes, fixing them, rinse and repeat; or, perhaps fuzzing is run in a batch over, say, a weekend when the test machine is available.
The current research approach is batch based, not fixing any of the faults discovered (earlier researchers fixed faults).
Not fixing discovered faults means that underlying coding mistakes may be repeatedly encountered, which wastes cpu time because many fuzzers terminate the run when the program they are testing crashes (a program crash is a commonly encountered fuzzing fault experience). The plot below shows the number of occurrences of the same underlying coding mistake, when running eight fuzzers on the program JasPer; 77 distinct coding mistakes were discovered, with three fuzzers run over 3,000 times, four run over 1,500 times, and one run 62 times (see Green Fuzzing: A Saturation-based Stopping Criterion using Vulnerability Prediction by Lipp, Elsner, Kacianka, Pretschner, Böhme, and Banescu; code+data):
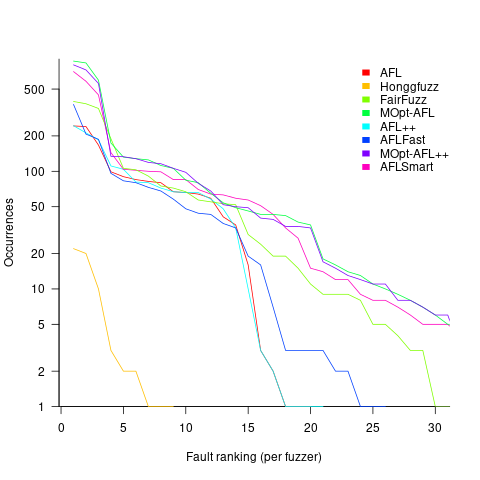
I have not seen any paper where the researchers attempt to reduce the number of times the same root cause coding mistake is discovered. Researchers are focused on discovering unreported faults; and with around 98% of fault discoveries being duplicates, appear to have resources to squander.
If developers primarily use a find/fix iterative process, then duplicate discoveries will be an annoying drag on cpu time. However, duplicate discoveries are going to make it difficult to effectively benchmark fuzzers.
WebAssembly vs JavaScript performance: 2023 edition
WebAssembly is an assembly-like language intended to be executed by web browsers on an internal stack machine. The intent is that compilers for high-level languages (i.e., C, Cobol, and C#) treat WebAssembly just like they would the assembly language of a cpu. Some substantial applications have been ported, e.g., the R statistical environment, which is written in C and Fortran.
Some people claim that WebAssembly based applications will run faster, and consume less power, than those written in JavaScript or PHP. Now, one virtual machine is as much like any other. Performance differences are driven by compiler optimizations, the ease with which particular language features can be mapped to the available instructions, and an application’s use of easy/hard to map high-level language features.
Researchers have run benchmarks to compare the runtime performance and power consumption of Wasm against other browser based languages, and this post analyses the runtime performance results from two papers.
TL;DR: Relative performance for Wasm/JavaScript varies across browsers and programs. Everything interacts with everything else, which makes analysis complicated.
As is the case with most data analysis in software engineering, the researchers used rudimentary statistical techniques (which is a shame given the huge effort that went into collecting the data). The conclusions of both papers is that for WebAssembly/JavaScript, relative performance issues are complicated, but the techniques they used did not enable them to understand why.
What kind of statistical techniques are applicable for analysing these benchmarks?
Use of different languages/browsers might be expected to have some percentage impact on performance, e.g., programs written in language X will be p% faster/slower. The following equation is one modelling approach, and this equation can be fitted using nonlinear regression:
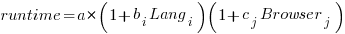 , where:
, where: 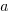 is a constant,
is a constant, 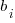 is the fitted constant for language
is the fitted constant for language 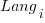 , and
, and 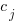 is the fitted constant for browser
is the fitted constant for browser 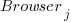
The problem with this equation is that it involves a separate equation for each combination of language/browser (assuming that all benchmarks are bundled together in the value of 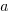 ). It is possible to use a single equation when there are just two languages/two browsers, by mapping them to the values 0/1.
). It is possible to use a single equation when there are just two languages/two browsers, by mapping them to the values 0/1.
All languages/browsers/benchmarks can be included in a single linear regression model by treating them as factors in a log transformed model; the equation is: 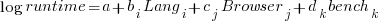 , where:
, where: 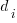 is the fitted constant for benchmark
is the fitted constant for benchmark 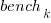 . The values of
. The values of 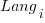 ,
, 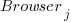 , and
, and 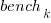 are zero, or one for the corresponding fitted constant. All the factors on the right-hand-side are discrete, so a log transform has nothing to distort.
are zero, or one for the corresponding fitted constant. All the factors on the right-hand-side are discrete, so a log transform has nothing to distort.
The fitted equation can then be transformed to:
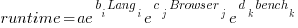
This model assumes that each factor is independent of the others, i.e., the relative performance of each language does not depend on the browser, and that relative performance does not significantly vary between benchmarks, e.g., if  runs 10% faster when implemented in
runs 10% faster when implemented in  , then
, then  also runs close to 10% faster when implemented in
also runs close to 10% faster when implemented in  .
.
How well did the benchmark data from the two papers fit this model, and what were the performance numbers?
The study WebAssembly versus JavaScript: Energy and Runtime Performance by De Macedo, Abreu, Pereira, and Saraiva ran a wide range of benchmarks. It compared C/Wasm/JavaScript running on Chrome/Firefox/Edge. One set of benchmarks were 10 small compute-intensive programs (in Wasm/JavaScript), which were executed with small/medium/large amounts of input data; the other set of benchmarks were two large applications WasmBoy is a Game-boy/Gameboy Color Emulator (written in Typescript and compiled to Wasm), and PSPDFKit supporting viewing, annotating, and filling in forms in PDF documents (written in C/C++ and compiled to a both a subset of JavaScript and Wasm).
Results from the 10 small benchmarks showed strong interactions between browser and language (i.e., Wasm performance relative to JavaScript, varied between browsers; with Edge being faster and Firefox being slower), and a lot of interaction between benchmark and input data size. Support for Wasm is relatively new, relative to the much more mature JavaScript, so it’s not surprising that different browsers have different performance; I’m arm waving when I say that the input size dependency may be related to JIT issues (code).
When interactions are included, the fitted equation has the form:
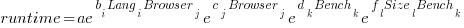
Analysing the results for the two applications, we find that:
- WasmBoy: the factors were independent, and WebAssembly was faster than JavaScript. The
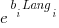 factor was 0.84 for Wasm and 1 for JavaScript,
factor was 0.84 for Wasm and 1 for JavaScript, - PSPDFKit: there was interaction between the language and browser, with behavior similar to that seen for the small benchmarks.
The study Comparing the Energy Efficiency of WebAssembly and JavaScript in Web Applications on Android Mobile Devices by van Hasselt, Huijzendveld, Noort, de Ruijter, Islam, and Malavolta compared the performance of WebAssembly/JavaScript running compute intensive benchmarks on Firefox/Chrome.
Fitting a regression model to the data from the eight benchmarks showed strong interactions between benchmark programs and language, with each language being faster for some programs (code).
It’s not surprising that the results failed to show a conclusive performance advantage for either WebAssembly or JavaScript, across benchmarks. The situation might change as the wasm virtual machine is tuned, and compilers targetting wasm implement a wider range of optimizations.
Update
A performance analysis of C, Rust, Go, and Javascript compiled to Webassembler
A comparison of C++ and Rust compiler performance
Large code bases take a long time to compile and build. How much impact does the choice of programming language have on compiler/build times?
The small number of industrial strength compilers available for the widely used languages makes the discussion as much about distinct implementations as distinct languages. And then there is the issue of different versions of the same compiler having different performance characteristics; for instance, the performance of Microsoft’s C++ Visual Studio compiler depends on the release of the compiler and the version of the standard specified.
Implementation details can have a significant impact on compile time. Compile time may be dominated by lexical analysis, while support for lots of fancy optimization shifts the time costs to code generation, and poorly chosen algorithms can result in symbol table lookup being a time sink (especially for large programs). For short programs, compile time may be dominated by start-up costs. These days, developers rarely have to worry about small memory size causing occurring when compiling a large source file.
A recent blog post compared the compile/build time performance of Rust and C++ on Linux and Apple’s OS X, and strager kindly made the data available.
The most obvious problem with attempting to compare the performance of compilers for different languages is that the amount of code contained in programs implementing the same functionality will differ (this is also true when the programs are written in the same language).
strager’s solution was to take a C++ program containing 9.3k LOC, plus 7.3K LOC of tests, and convert everything to Rust (9.5K LOC, plus 7.6K LOC of tests). In total, the benchmark consisted of compiling/building three C++ source files and three equivalent Rust source files.
The performance impact of number of lines of source code was measured by taking the largest file and copy-pasting it 8, 16, and 32 times, to create three every larger versions.
The OS X benchmarks did not include multiple file sizes, and are not included in the following analysis.
A variety of toolchain options were included in different runs, and for Rust various command line options; most distinct benchmarks were run 10 times each. On Linux, there were a total of 360 C++ runs, and for Rust 1,066 runs (code+data).
The model 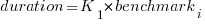 , where
, where 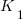 is a fitted regression constant, and
is a fitted regression constant, and 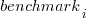 is the fitted regression coefficient for the
is the fitted regression coefficient for the 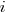 ‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
The model 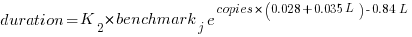 , where
, where 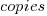 is the number of copies,
is the number of copies, 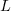 is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
The expression 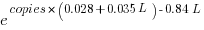 is a language and source code size multiplication factor. The numeric values are:
is a language and source code size multiplication factor. The numeric values are:
1 8 16 32 C++ 1.03 1.25 1.57 2.45 Rust 0.98 1.52 2.52 6.90 |
showing that while Rust compilation is faster than C++, for ‘shorter’ files, it becomes much relatively slower as the quantity of source increases.
The size factor for Rust is growing quadratically, while it is much closer to linear for C++.
What are the threats to the validity of this benchmark comparison?
The most obvious is the small number of files benchmarked. I don’t have any ideas for creating a larger sample.
How representative is the benchmark of typical projects? An explicit goal in benchmark selection was to minimise external dependencies (to reduce the effort likely to be needed to translate to Rust). Typically, projects contain many dependencies, with compilers sometimes spending more time processing dependency information than compiling the actual top-level source, e.g., header files in C++.
A less obvious threat is the fact that the benchmarks for each language were run in contiguous time intervals, i.e., all Rust, then all C++, then all Rust (see plot below; code+data):

It is possible that one or more background processes were running while one set of language benchmarks was being run, which would skew the results. One solution is to intermix the runs for each language (switching off all background tasks is much harder).
I was surprised by how well the regression model fitted the data; the fit is rarely this good. Perhaps a larger set of benchmarks would increase the variance.
Fitting discontinuous data from disparate sources
Sorting and searching are probably the most widely performed operations in computing; they are extensively covered in volume 3 of The Art of Computer Programming. Algorithm performance is influence by the characteristics of the processor on which it runs, and the size of the processor cache(s) has a significant impact on performance.
A study by Khuong and Morin investigated the performance of various search algorithms on 46 different processors. Khuong The two authors kindly sent me a copy of the raw data; the study webpage includes lots of plots.
The performance comparison involved 46 processors (mostly Intel x86 compatible cpus, plus a few ARM cpus) times 3 array datatypes times 81 array sizes times 28 search algorithms. First a 32/64/128-bit array of unsigned integers containing N elements was initialized with known values. The benchmark iterated 2-million times around randomly selecting one of the known values, and then searching for it using the algorithm under test. The time taken to iterate 2-million times was recorded. This was repeated for the 81 values of N, up to 63,095,734, on each of the 46 processors.
The plot below shows the results of running each algorithm benchmarked (colored lines) on an Intel Atom D2700 @ 2.13GHz, for 32-bit array elements; the kink in the lines occur roughly at the point where the size of the array exceeds the cache size (all code+data):
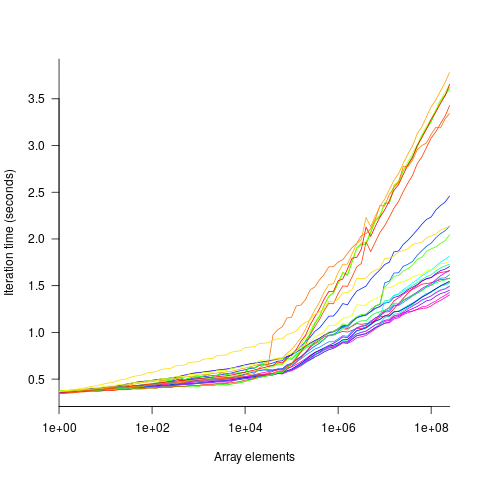
What is the most effective way of analyzing the measurements to produce consistent results?
One approach is to build two regression models, one for the measurements before the cache ‘kink’ and one for the measurements after this kink. By adding in a dummy variable at the kink-point, it is possible to merge these two models into one model. The problem with this approach is that the kink-point has to be chosen in advance. The plot shows that the performance kink occurs before the array size exceeds the cache size; other variables are using up some of the cache storage.
This approach requires fitting 46*3=138 models (I think the algorithm used can be integrated into the model).
If data from lots of processors is to be fitted, or the three datatypes handled, an automatic way of picking where the first regression model should end, and where the second regression model should start is needed.
Regression discontinuity design looks like it might be applicable; treating the point where the array size exceeds the cache size as the discontinuity. Traditionally discontinuity designs assume a sharp discontinuity, which is not the case for these benchmarks (R’s rdd package worked for one algorithm, one datatype running on one processor); the more recent continuity-based approach supports a transition interval before/after the discontinuity. The R package rdrobust supports a continued-based approach, but seems to expect the discontinuity to be a change of intercept, rather than a change of slope (or rather, I could not figure out how to get it to model a just change of slope; suggestions welcome).
Another approach is to use segmented regression, i.e., one of more distinct lines. The package segmented supports fitting this kind of model, and does estimate what they call the breakpoint (the user has to provide a first estimate).
I managed to fit a segmented model that included all the algorithms for 32-bit data, running on one processor (code+data). Looking at the fitted model I am not hopeful that adding data from more than one processor would produce something that contained useful information. I suspect that there are enough irregular behaviors in the benchmark runs to throw off fitting quality.
I’m always asking for more data, and now I have more data than I know how to analyze in a way that does not require me to build 100+ models 🙁
Suggestions welcome.
Benchmarking desktop PCs circa 1990
Before buying a computer customers want to be confident of choosing the best they can get for the money, and performance has often been a major consideration. Computer benchmark performance results were once widely discussed.
Knight’s analysis of early mainframe performance was widely cited for many years.
Performance on the Byte benchmarks was widely cited before Intel started spending billions on advertising, clock frequency has not always had the brand recognition it has today.
The Byte benchmark was originally designed for Intel x86 processors running Microsoft DOS; The benchmark was introduced in the June 1985 issue, and was written in the still relatively new C language (earlier microprocessor benchmarks were often written in BASIC, because early micros often came with a free BASIC interpreter), it was updated in the 1990s to be Windows based, and implemented for Unix.
Benchmarking computers using essentially the same cpu architecture and operating system removes many complications that have to be addressed when these differ. Before Wintel wiped them out, computers from different manufacturers (and often the same manufacturer) contained completely different cpu architectures, ran different operating systems, and compilers were usually created in-house by the manufacturer (or some university who got a large discount on their computer purchase).
The Fall 1990 issue of Byte contains tables of benchmark results from 1988-90. What can we learn from these results?
The most important takeaway from the tables is that those performing the benchmarks appreciated the importance of measuring hardware performance using the applications that customers are likely to be running on their computer, e.g., word processors, spreadsheets, databases, scientific calculations (computers were still sufficiently niche back then that scientific users were a non-trivial percentage of the market), and compiling (hackers were a large percentage of Byte’s readership).
The C benchmarks attempted to measure CPU, FPU (built-in hardware support for floating-point arrived with the 486 in April 1989, prior to that it was an add-on chip that required spending more money), Disk and Video (at the time support for color was becoming mainstream, but bundled hardware graphics support still tended to be minimal).
Running the application benchmarks takes a lot of time, plus the necessary software (which takes time to install from floppies, the distribution technology of the day). Running the C benchmarks is much quicker and simpler.
Ideally the C benchmarks are a reliable stand-in for the application benchmarks (meaning that only the C benchmarks need be run).
Let’s fit some regression models to the measurements of the 61 systems benchmarked, all supporting hardware floating-point (code+data). Surprisingly there is no mention of such an exercise being done by the Byte staff, even though one of the scientific benchmarks included regression fitting.
The following fitted equations explain around 90% of the variance of the data, i.e., they are good fits.
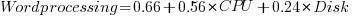
For wordprocessing, the CPU benchmark explains around twice as much as the Disk benchmark.
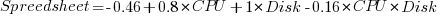
For spreadsheets, CPU and Disk contribute about the same.
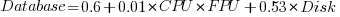
Database is nearly all Disk.
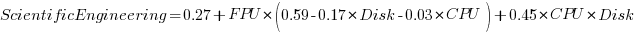
Scientific/Engineering is FPU, plus interactions with other components.
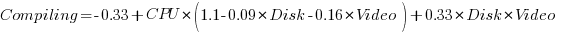
Compiling is CPU, plus interactions with other components.
Byte’s benchmark reports were great eye candy, and readers probably took away a rough feel for the performance of various systems. Perhaps somebody at the time also fitted regression models to the data. The magazine contained plenty of adverts for software to do this.
Modeling visual studio C++ compile times
Last week I spotted an interesting article on the compile-time performance of C++ compilers running under Microsoft Windows. The author had obviously put a lot of work into gathering the data, and had taken care to have multiple runs to reduce the impact of random effects (128 runs to be exact); but, as if often the case, the analysis of the data was lackluster. I posted a comment asking for the data, and a link was posted the next day 🙂
The compilers benchmarked were: Visual Studio 2015, Visual Studio 2017 and clang 7.0.1; the compilers were configured to target: C++20, C++17, C++14, C++11, C++03, or C++98. The source code used was 100 system headers.
If we are interested in understanding the contribution of each component to overall compile-time, the obvious fist regression model to build is:
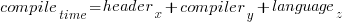
where: 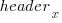 are the different headers,
are the different headers, 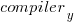 the different compilers and
the different compilers and 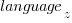 the different target languages. There might be some interaction between variables, so something more complicated was tried first; the final fitted model was (code+data):
the different target languages. There might be some interaction between variables, so something more complicated was tried first; the final fitted model was (code+data):
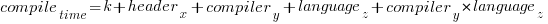
where 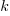 is a constant (the
is a constant (the Intercept in R’s summary output). The following is a list of normalised numbers to plug into the equation (clang is the default compiler and C++03 the default language, and so do not appear in the list, the : symbol represents the multiplication; only a few of the 100 headers are listed, details are available):
Estimate Std. Error t value Pr(>|t|) (Intercept) headerany 1.000000000 0.051100398 headerarray headerassert.h 0.522336397 -0.654056185 ... headerwctype.h headerwindows.h -0.648095154 1.304270250 compilerVS15 compilerVS17 -0.185795534 -0.114590143 languagec++11 languagec++14 0.032930014 0.156363433 languagec++17 languagec++20 0.192301727 0.184274629 languagec++98 compilerVS15:languagec++11 0.001149643 -0.058735591 compilerVS17:languagec++11 compilerVS15:languagec++14 -0.038582437 -0.183708714 compilerVS17:languagec++14 compilerVS15:languagec++17 -0.164031495 NA compilerVS17:languagec++17 compilerVS15:languagec++20 -0.181591418 NA compilerVS17:languagec++20 compilerVS15:languagec++98 -0.193587045 0.062414667 compilerVS17:languagec++98 0.014558295 |
As an example, the (normalised) time to compile wchar.h using VS15 with languagec++11 is:
1-0.514807638-0.183862162+0.033951731-0.059720131
Each component adds/substracts to/from the normalised mean.
Building this model didn’t take long. While waiting for the kettle to boil, I suddenly realised that an additive model was probably inappropriate for this problem; oops. Surely the contribution of each component was multiplicative, i.e., components have a percentage impact to performance.
A quick change to the form of the fitted model:
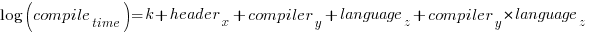
Taking the exponential of both side, the fitted equation becomes:
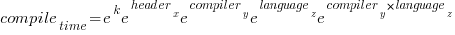
The numbers, after taking the exponent, are:
(Intercept) headerany 9.724619e+08 1.051756e+00 ... headerwctype.h headerwindows.h 3.138361e-01 2.288970e+00 compilerVS15 compilerVS17 7.286951e-01 7.772886e-01 languagec++11 languagec++14 1.011743e+00 1.049049e+00 languagec++17 languagec++20 1.067557e+00 1.056677e+00 languagec++98 compilerVS15:languagec++11 1.003249e+00 9.735327e-01 compilerVS17:languagec++11 compilerVS15:languagec++14 9.880285e-01 9.351416e-01 compilerVS17:languagec++14 compilerVS15:languagec++17 9.501834e-01 NA compilerVS17:languagec++17 compilerVS15:languagec++20 9.480678e-01 NA compilerVS17:languagec++20 compilerVS15:languagec++98 9.402461e-01 1.058305e+00 compilerVS17:languagec++98 1.001267e+00 |
Taking the same example as above: wchar.h using VS15 with c++11. The compile-time (in cpu clock cycles) is:
9.724619e+08*3.138361e-01*7.286951e-01*1.011743e+00*9.735327e-01
Now each component causes a percentage change in the (mean) base value.
Both of these model explain over 90% of the variance in the data, but this is hardly surprising given they include so much detail.
In reality compile-time is driven by some combination of additive and multiplicative factors. Building a combined additive and multiplicative model is going to be like wrestling an octopus, and is left as an exercise for the reader 🙂
Given a choice between these two models, I think the multiplicative model is probably closest to reality.
Building a regression model is easy and informative
Running an experiment is very time-consuming. I am always surprised that people put so much effort into gathering the data and then spend so little effort analyzing it.
The Computer Language Benchmarks Game looks like a fun benchmark; it compares the performance of 27 languages using various toy benchmarks (they could not be said to be representative of real programs). And, yes, lots of boxplots and tables of numbers; great eye-candy, but what do they all mean?
The authors, like good experimentalists, make all their data available. So, what analysis should they have done?
A regression model is the obvious choice and the following three lines of R (four lines if you could the blank line) build one, providing lots of interesting performance information:
cl=read.csv("Computer-Language_u64q.csv.bz2", as.is=TRUE)
cl_mod=glm(log(cpu.s.) ~ name+lang, data=cl)
summary(cl_mod) |
The following is a cut down version of the output from the call to summary, which summarizes the model built by the call to glm.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.299246 0.176825 7.348 2.28e-13 ***
namechameneosredux 0.499162 0.149960 3.329 0.000878 ***
namefannkuchredux 1.407449 0.111391 12.635 < 2e-16 ***
namefasta 0.002456 0.106468 0.023 0.981595
namemeteor -2.083929 0.150525 -13.844 < 2e-16 ***
langclojure 1.209892 0.208456 5.804 6.79e-09 ***
langcsharpcore 0.524843 0.185627 2.827 0.004708 **
langdart 1.039288 0.248837 4.177 3.00e-05 ***
langgcc -0.297268 0.187818 -1.583 0.113531
langocaml -0.892398 0.232203 -3.843 0.000123 ***
Null deviance: 29610 on 6283 degrees of freedom
Residual deviance: 22120 on 6238 degrees of freedom
What do all these numbers mean?
We start with glm's first argument, which is a specification of the regression model we are trying to fit: log(cpu.s.) ~ name+lang
cpu.s. is cpu time, name is the name of the program and lang is the language. I found these by looking at the column names in the data file. There are other columns in the data, but I am running in quick & simple mode. As a first stab, I though cpu time would depend on the program and language. Why take the log of the cpu time? Well, the model fitted using cpu time was very poor; the values range over several orders of magnitude and logarithms are a way of compressing this range (and the fitted model was much better).
The model fitted is:
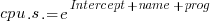 , or
, or 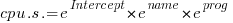
Plugging in some numbers, to predict the cpu time used by say the program chameneosredux written in the language clojure, we get: 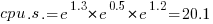 (values taken from the first column of numbers above).
(values taken from the first column of numbers above).
This model assumes there is no interaction between program and language. In practice some languages might perform better/worse on some programs. Changing the first argument of glm to: log(cpu.s.) ~ name*lang, adds an interaction term, which does produce a better fitting model (but it's too complicated for a short blog post; another option is to build a mixed-model by using lmer from the lme4 package).
We can compare the relative cpu time used by different languages. The multiplication factor for clojure is 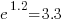 , while for
, while for ocaml it is 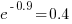 . So
. So clojure consumes 8.2 times as much cpu time as ocaml.
How accurate are these values, from the fitted regression model?
The second column of numbers in the summary output lists the estimated standard deviation of the values in the first column. So the clojure value is actually 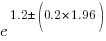 , i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the
, i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the ocaml values are 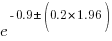 , between 0.3 and 0.6.
, between 0.3 and 0.6.
The fourth column of numbers is the p-value for the fitted parameter. A value of lower than 0.05 is a common criteria, so there are question marks over the fit for the program fasta and language gcc. In fact many of the compiled languages have high p-values, perhaps they ran so fast that a large percentage of start-up/close-down time got included in their numbers. Something for the people running the benchmark to investigate.
Isn't it easy to get interesting numbers by building a regression model? It took me 10 minutes, ok I spend a lot of time fitting models. After spending many hours/days gathering data, spending a little more time learning to build simple regression models is well worth the effort.
Cost/performance analysis of 1944-1967 computers: Knight’s data
Changes In Computer Performance and Evolving Computer Performance 1963-1967, by Kenneth Knight, are the references to cite when discussing the performance of early computers. I suspect that very few people have read the two papers they are citing (citing without reading is a surprisingly common practice). Both papers were published in Datamation, a computer magazine whose technical contents could rival that of the ACM journals in the 1960s, but later becoming more of a trade magazine. Until the articles appeared on bitsavers.org they were only really available through national or major regional libraries.
Both papers contain lots of interesting performance and cost data on computers going back to the 1940s. However, I was not interested enough to type in all that data. This week I found high quality OCRed copies of the papers on the Internet Archive; my effort was reduced to fixing typos, which felt like less work.
So let’s try to reproduce Knight’s analysis of the data (code and data). Working in the mid-1960s I imagine Knight did everything manually, with the help of mechanical calculators. I have the advantage of fancy software, a very fast computer and techniques that were invented after Knight did his analysis (e.g., generalized linear methods).
Each paper contains its own dataset: the first contains performance+cost data on 225 computers available between 1944 and 1963, while the second contains this information on 63 computers available between 1963 and 1967.
The dataset lists the computer name, the date it was introduced, number of operations per second and the number of seconds that can be rented for a dollar (most computer time used to be rented, then 25 years later personal computers came along and people got to own one, now 25 years after that Cloud is causing a switch back to rental per second).
How are operations measured? The MIPS unit of measurement did not start to be generally used until the 1980s. Knight used 30 or so system characteristics, such as time to perform various arithmetic operations and I/O time, plus characteristics of scientific and commercial applications to calculate a value considered to be a representative scientific or commercial operation.
There is no mention of how seconds-per-dollar values were obtained. Did Knight ask customers or vendors? In a rental market I imagine vendor pricing could be very flexible.
In the 1970s people started talking about Moore’s law, but in the 1960s there was Grosch’s law: Computer performance increases as the square of the cost, i.e., faster computers were cheaper to rent, for a given number of operations. Knight set out to empirically check Grosch’s law, i.e., he was looking for a quadratic fit.
Fitting a regression model to the 1950-1961 data, Knight obtained an exponent of 2.18, while I obtained 2.38 for commercial operations (using a slightly more sophisticated model, because I could); time on faster computers was cheaper than Grosch claimed. For scientific operations Knight obtained 1.92, while I obtained 3.56; despite trying all sorts of jiggery-pokery I could not get a lower value. Unless Knight used very different values to the ones published in the ‘scientific’ columns, one of us has made a big mistake (please let me know if my code is wrong).
Fitting a regression model to the 1963-1967 data, I get figures (both around 2.85 and 2.94) that are roughly in agreement with Knight (2.5 and 3.1). Grosch’s law has broken down by 1963 (if it ever held for scientific operations).
The plot below shows operations per second against operations per dollar for the 1953-1961 data, with fitted lines for some specific years. It shows that while customers get fewer seconds per dollar on faster computers, the number of operations performed in those seconds is raised to the power of two+.
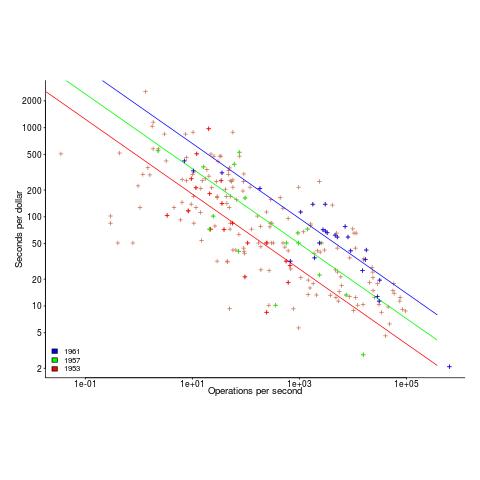
What other information can be extracted from the data? The 1953-1961 data shows seconds per dollar increased, over the whole performance range, by a factor of 1.15 per year, i.e., 15%, for both scientific and commercial; the 1963-1967 year on year increase jumps around a lot.
Recent Comments