Archive
Who are the famous academics in software engineering?
Who are today’s ‘famous’ academics in software engineering?
Famous as in, you can mention their name when chatting with general software developers, and expect those present to have heard of them, or you have heard their names dropped into a conversation, say, at least 3+ times this year (I’m excluding academics who are famous within one specific niche of software engineering). Academic, as in, works in an institution of secondary or tertiary higher learning.
When I started out in industry, the works of Knuth and Dijkstra were cited (not always accurately), people would talk about Ted Codd’s latest position on how best to structure a database. Tony Hoare later became known through his books, and Leslie Lamport for distributed systems and perhaps LaTeX. In very large niches, William Kahan for numerical analysis, and Barbara Liskov for the Liskov substitution principle.
Anyone suggesting Kernighan and Ritchie, of C and Unix fame, is overlooking the fact they worked in an industrial research lab.
A book series continues to maintain Knuth’s fame, while Dijkstra kept himself in the news by being a source of controversial quotes for industry journalists, and for kicking off the Go-To statement considered harmful debate (the latter is likely the reason that anybody has heard of him today). Has Kahan escaped his niche, even though use of floating-point arithmetic is now perhaps even more niche than it used to be?
How might academics become famous?
Widely used algorithms/metrics/techniques named after a person generates a kind of anonymous name recognition. For instance, Halstead complexity metric and McCabe’s cyclomatic complexity metric, and from the 1990s Shor’s algorithm.
Some people achieve fame through their association with a language. Academic name/language pairs include: McCarthy/Lisp, Wirth/Pascal, Stroustrup/C++ (worked in industry, university, industry, university), Peyton Jones/Haskell (university, industrial research, industry), Leroy/OCaml, Meyer/Eiffel.
An influential book, or widely read blog can generate a kind of fame.
Many academics have written an ‘algorithms’ book, and readers may have fond memories of the particular book they used as an undergraduate. Barry Boehm wrote “Software Engineering Economics”, but is more likely to be known for the model he spent his life promoting, i.e., the COCOMO model.
Fred Brooks, author of one of the most famous books in software engineering The Mythical Man Month, was not an academic worked in industry and then academia.
I have always been surprised by how many Turing award winners I have never heard of, or while recognizing a name am completely unfamiliar with their work. I am less surprised by my failure to recognise around half the names in the Wikipedia category software engineering researchers.
A few people are known because of the widespread use of their software (Linus Torvalds has never been an academic). Richard Stallman, employed as an academic, originally became famous as the author of the GNU version of emacs and gcc; the fame from the Free Software Foundation came after copyleft took off.
Are there academics who have become ‘famous’ in software engineering this century? I’m not in a position to answer this because I don’t read introductory software books, and generally avoid bike-shed discussions.
Does the resurgence of interest in AI mean that Judea Pearl’s fame is no longer niche?
I do read recent academic papers, and the only person on the list of most frequently cited authors in my evidence-based software engineering book with any claim to fame, researches cognitive neuroscience, i.e., Stanislas Dehaene.
Is software engineering a field where it is possible for a person, academic or otherwise, to become famous?
If there are fame worthy discoveries waiting to be made, or fame worthy software engineering book waiting to be written, how likely is it that the people responsible will be academics? A lot of the advances in software engineering have been made and continue to be made by those working in industry.
Suggestions relating to (in)famous academics welcome.
Anthropology and building software systems
Software systems are built by people, who are usually a member of one or more teams. While a lot of research effort has gone into studying the software/hardware used to build these systems, almost no effort has been invested in studying the activities of the people involved.
The study of human behaviors and cultures, in the broadest sense, sits within the field of Anthropology. The traditional image of an Anthropologist is someone who spends an extended period living with some remote tribe, publishing a monograph about their experiences on return to ‘civilisation’. In practice, anthropologists also study local tribes, such as professional workers.
Studies of the computer industry, by anthropologists, include: Global “Body Shopping” An Indian Labor System in the Information Technology Industry by Xiang Biao, and Cultures@SiliconValley by J. A. English-Lueck.
Reporters and professional authors sometimes write popular books for a general audience, which might be labelled pop anthropology. For instance, Kidder’s The Soul of a New Machine.
These academic/reporter publications are usually written by outsiders for an audience of outsiders. They are not intended to provide insights for insiders (Kidder’s book strikes me as reporting on the chaos that ensues when dysfunctional teams have to work together, which is not how it is described on its back cover).
If insiders want to learn about their community, some degree of insider knowledge is needed; exploring culture from the point of view of the subject of the study is known as Ethnography. Acquiring this knowledge can take years, an investment that will deter most researchers. Insightful insider commentary is most likely to come from insiders.
These days, insiders who write usually have blogs. Gerald Weinberg was an insider of times gone by, who wrote popular books for insiders about consulting in the software business; perhaps the most well known being “The Psychology of Computer Programming” (which really ought to be titled “The Sociology of Computer Programming”).
Who might be the consumers of research by anthropologists of software system development (assuming that a non-trivial amount eventually gets done)?
There are important outsiders, such as lawmakers looking to regulate.
Insiders only ever get to experience a sliver of the culture of software communities. The considered experiences of others can provide interesting insights, in particular learning about how teams working within other application domains operate.
Those seeking to change company culture ought to be looking to anthropology as a source of ideas for things that might work, or not.
History deals with the outcomes of past human behavior and culture, and there are a handful of historians of computing.
An evidence-based software engineering book from 2002
I recently discovered the book A Handbook of Software and Systems Engineering: Empirical Observations, Laws and Theories by Albert Endres and Dieter Rombach, completed in 2002.
The preface says: “This book is about the empirical aspects of computing. … we intend to look for rules and laws, and their underlying theories.” While this sounds a lot like my Evidence-based Software Engineering book, the authors take a very different approach.
The bulk of the material consists of a detailed discussion of 50 ‘laws’, 25 hypotheses and 12 conjectures based on the template: 1) a highlighted sentence making some claim, 2) Applicability, i.e., situations/context where the claim is likely to apply, 3) Evidence, i.e., citations and brief summary of studies.
As researchers of many years standing, I think the authors wanted to present a case that useful things had been discovered, even though the data available to them is nowhere near good enough to be considered convincing evidence for any of the laws/hypotheses/conjectures covered. The reasons I think this book is worth looking at are not those intended by the authors; my reasons include:
- the contents mirror the unquestioning mindset that many commercial developers have for claims derived from the results of software research experiments, or at least the developers I talk to about software research. I’m forever educating developers about the need for replications (the authors give a two paragraph discussion of the importance of replication), that sample size is crucial, and using professional developers as subjects.
Having spent twelve chapters writing authoritatively on 50 ‘laws’, 25 hypotheses and 12 conjectures, the authors conclude by washing their hands: “The laws in our set should not be seen as dogmas: they are not authoritatively asserted opinions. If proved wrong by objective and repeatable observations, they should be reformulated or forgotten.”
For historians of computing this book is a great source for the software folklore of the late 20th/early 21st century,
- the Evidence sections for each of the laws/hypotheses/conjectures is often unintentionally damming in its summary descriptions of short/small experiments involving a handful of people or a few hundred lines of code. For many, I would expect the reaction to be: “Is that it?”
Previously, in developer/researcher discussions, if a ‘fact’ based on the findings of long ago software research is quoted, I usually explain that it is evidence-free folklore; followed by citing The Leprechauns of Software Engineering as my evidence. This book gives me another option, and one with greater coverage of software folklore,
- the quality of the references, which are often to the original sources. Researchers tend to read the more recently published papers, and these are the ones they often cite. Finding the original work behind some empirical claim requires following the trail of citations back in time, which can be very time-consuming.
Endres worked for IBM from 1957 to 1992, and was involved in software research; he had direct contact with the primary sources for the software ‘laws’ and theories in circulation today. Romback worked for NASA in the 1980s and founded the Fraunhofer Institute for Experimental Software Engineering.
The authors cannot be criticized for the miniscule amount of data they reference, and not citing less well known papers. There was probably an order of magnitude less data available to them in 2002, than there is available today. Also, search engines were only just becoming available, and the amount of material available online was very limited in the first few years of 2000.
I started writing a book in 2000, and experienced the amazing growth in the ability of search engines to locate research papers (first using AltaVista and then Google), along with locating specialist books with Amazon and AbeBooks. I continued to use university libraries for papers, which I did not use for the evidence-based book (not that this was a viable option).
4,000 vs 400 vs 40 hours of software development practice
What is the skill difference between professional developers and newly minted computer science graduates?
Practice, e.g., 4,000 vs. 400 hours
People get better with practice, and after two years (around 4,000 hours) a professional developer will have had at least an order of magnitude more practice than most students; not just more practice, but advice and feedback from experienced developers. Most of these 4,000 hours are probably not the deliberate practice of 10,000 hours fame.
It’s understandable that graduates with a computing degree consider themselves to be proficient software developers; this opinion is based on personal experience (i.e., working with other students like themselves), and not having spent time working with professional developers. It’s not a joke that a surprising number of academics don’t appreciate the student/professional difference, the problem is that some academics only ever get to see a limit range of software development expertise (it’s a question of incentives).
Surveys of student study time have found that for Computer science, around 50% of students spend 11 hours or more, per week, in taught study and another 11 hours or more doing independent learning; let’s take 11 hours per week as the mean, and 30 academic weeks in a year. How much of the 330 hours per year of independent learning time is spent creating software (that’s 1,000 hours over a three-year degree, assuming that any programming is required)? I have no idea, and picked 40% because it matched up with 4,000.
Based on my experience with recent graduates, 400 hours sounds high (I have no idea whether an average student spends 4-hours per week doing programming assignments). While a rare few are excellent, most are hopeless. Perhaps the few hours per week nature of their coding means that they are constantly relearning, or perhaps they are just cutting and pasting code from the Internet.
Most graduates start their careers working in industry (around 50% of comp sci/maths graduates work in an ICT profession; UK higher-education data), which means that those working in industry are ideally placed to compare the skills of recent graduates and professional developers. Professional developers have first-hand experience of their novice-level ability. This is not a criticism of computing degrees; there are only so many hours in a day and lots of non-programming material to teach.
Many software developers working in industry don’t have a computing related degree (I don’t). Lots of non-computing STEM degrees give students the option of learning to program (I had to learn FORTRAN, no option). I don’t have any data on the percentage of software developers with a computing related degree, and neither do I have any data on the average number of hours non-computing STEM students spend on programming; I’ve cosen 40 hours to flow with the sequence of 4’s (some non-computing STEM students spend a lot more than 400 hours programming; I certainly did). The fact that industry hires a non-trivial number of non-computing STEM graduates as software developers suggests that, for practical purposes, there is not a lot of difference between 400 and 40 hours of practice; some companies will take somebody who shows potential, but no existing coding knowledge, and teach them to program.
Many of those who apply for a job that involves software development never get past the initial screening; something like 80% of people applying for a job that specifies the ability to code, cannot code. This figure is based on various conversations I have had with people about their company’s developer recruitment experiences; it is not backed up with recorded data.
Some of the factors leading to this surprisingly high value include: people attracted by the salary deciding to apply regardless, graduates with a computing degree that did not require any programming (there is customer demand for computing degrees, and many people find programming is just too hard for them to handle, so universities offer computing degrees where programming is optional), concentration of the pool of applicants, because those that can code exit the applicant pool, leaving behind those that cannot program (who keep on applying).
Apologies to regular readers for yet another post on professional developers vs. students, but I keep getting asked about this issue.
Anthropological studies of software engineering
Anthropology is the study of humans, and as such it is the top level research domain for many of the human activities involved in software engineering. What has been discovered by the handful of anthropologists who have spent time researching the tiny percentage of humans involved in writing software?
A common ‘discovery’ is that developers don’t appear to be doing what academics in computing departments claim they do; hardly news to those working in industry.
The main subfields relevant to software are probably: cultural anthropology and social anthropology (in the US these are combined under the name sociocultural anthropology), plus linguistic anthropology (how language influences social life and shapes communication). There is also historical anthropology, which is technically what historians of computing do.
For convenience, I’m labelling anybody working in an area covered by anthropology as an anthropologist.
I don’t recommend reading any anthropology papers unless you plan to invest a lot of time in some subfield. While I have read lots of software engineering papers, anthropologist’s papers on this topic are often incomprehensible to me. These papers might best be described as anthropology speak interspersed with software related terms.
Anthropologists write books, and some of them are very readable to a more general audience.
The Art of Being Human: A Textbook for Cultural Anthropology by Wesch is a beginner’s introduction to its subject.
Ethnography, which explores cultural phenomena from the point of view of the subject of the study, is probably the most approachable anthropological research. Ethnographers spend many months living with a remote tribe, community, or nowadays a software development company, and then write-up their findings in a thesis/report/book. Examples of approachable books include: “Engineering Culture: Control and Commitment in a High-Tech Corporation” by Kunda, who studied a large high-tech company in the mid-1980s; “No-Collar: The Humane Workplace and its Hidden Costs” by Ross, who studied an internet startup that had just IPO’ed, and “Coding Freedom: The Ethics and Aesthetics of Hacking” by Coleman, who studied hacker culture.
Linguistic anthropology is the field whose researchers are mostly likely to match developers’ preconceived ideas about what humanities academics talk about. If I had been educated in an environment where Greek and nineteenth century philosophers were the reference points for any discussion, then I too would use this existing skill set in my discussions of source code (philosophers of source code did not appear until the twentieth century). Who wouldn’t want to apply hermeneutics to the interpretation of source code (the field is known as Critical code studies)?
It does not help that the software knowledge of many of the academics appears to have been acquired by reading computer books from the 1940s and 1950s.
The most approachable linguistic anthropology book I have found, for developers, is: The Philosophy of Software Code and Mediation in the Digital Age by Berry (not that I have skimmed many).
Research software code is likely to remain a tangled mess
Research software (i.e., software written to support research in engineering or the sciences) is usually a tangled mess of spaghetti code that only the author knows how to use. Very occasionally I encounter well organized research software that can be used without having an email conversation with the author (who has invariably spent years iterating through many versions).
Spaghetti code is not unique to academia, there is plenty to be found in industry.
Structural differences between academia and industry make it likely that research software will always be a tangled mess, only usable by the person who wrote it. These structural differences include:
- writing software is a low status academic activity; it is a low status activity in some companies, but those involved don’t commonly have other higher status tasks available to work on. Why would a researcher want to invest in becoming proficient in a low status activity? Why would the principal investigator spend lots of their grant money hiring a proficient developer to work on a low status activity?
I think the lack of status is rooted in researchers’ lack of appreciation of the effort and skill needed to become a proficient developer of software. Software differs from that other essential tool, mathematics, in that most researchers have spent many years studying mathematics and understand that effort/skill is needed to be able to use it.
Academic performance is often measured using citations, and there is a growing move towards citing software,
- many of those writing software know very little about how to do it, and don’t have daily contact with people who do. Recent graduates are the pool from which many new researchers are drawn. People in industry are intimately familiar with the software development skills of recent graduates, i.e., the majority are essentially beginners; most developers in industry were once recent graduates, and the stream of new employees reminds them of the skill level of such people. Academics see a constant stream of people new to software development, this group forms the norm they have to work within, and many don’t appreciate the skill gulf that exists between a recent graduate and an experienced software developer,
- paid a lot less. The handful of very competent software developers I know working in engineering/scientific research are doing it for their love of the engineering/scientific field in which they are active. Take this love away, and they will find that not only does industry pay better, but it also provides lots of interesting projects for them to work on (academics often have the idea that all work in industry is dull).
I have met people who have taken jobs writing research software to learn about software development, to make themselves more employable outside academia.
Does it matter that the source code of research software is a tangled mess?
The author of a published paper is supposed to provide enough information to enable their work to be reproduced. It is very unlikely that I would be able to reproduce the results in a chemistry or genetics paper, because I don’t know enough about the subject, i.e., I am not skilled in the art. Given a tangled mess of source code, I think I could reproduce the results in the associated paper (assuming the author was shipping the code associated with the paper; I have encountered cases where this was not true). If the code failed to build correctly, I could figure out (eventually) what needed to be fixed. I think people have an unrealistic expectation that research code should just build out of the box. It takes a lot of work by a skilled person to create to build portable software that just builds.
Is it really cost-effective to insist on even a medium-degree of buildability for research software?
I suspect that the lifetime of source code used in research is just as short and lonely as it is in other domains. One study of 214 packages associated with papers published between 2001-2015 found that 73% had not been updated since publication.
I would argue that a more useful investment would be in testing that the software behaves as expected. Many researchers I have spoken to have not appreciated the importance of testing. A common misconception is that because the mathematics is correct, the software must be correct (completely ignoring the possibility of silly coding mistakes, which everybody makes). Commercial software has the benefit of user feedback, for detecting some incorrect failures. Research software may only ever have one user.
Research software engineer is the fancy title now being applied to people who write the software used in research. Originally this struck me as an example of what companies do when they cannot pay people more, they give them a fancy title. Recently the Society of Research Software Engineering was setup. This society could certainly help with training, but I don’t see it making much difference with regard status and salary.
Update
This post generated a lot of discussion on the research software mailing list, and Peter Schmidt invited me to do a podcast with him. Here it is.
Waiting for the funerals: culture in software engineering research
A while ago I changed my opinion about why software engineering academics very rarely got/get involved in empirical/experimental based research.
I used to think it was because commercial data was so hard to get hold of.
In practice commercial data does not seem to be that hard to get hold of. At least for academics in business schools, and I have not experienced problems gaining access to commercial data (but it is very hard finding a company willing to allow me to make an anonymised version of its data public). There are many evidence-based papers published using confidential data (i.e., data that cannot be made public).
I now think the reasons for non-evidence-based research are culture and preference for non-people based research.
In the academic world the software side of computing often has a strong association is mathematics departments (I know that in some universities it is in engineering). I have had several researchers tell me that it would raise eyebrows, if they started doing more people oriented research, because this kind of research is viewed as being the purview of other departments.
Software had its algorithm era, which is now long gone; but unfortunately, many academics still live in a world where the mindset of TEOCP holds sway.
Baffled looks are common, when I talk to software engineering academics. They are baffled by the idea that it is possible to run experiments in software engineering, and they are baffled by the idea of evidence-based theories. I am still struggling to understand the mindset that produces the arguments they make against the possibility of experiments and evidence being useful.
In the past I know that some researchers have had problems getting experiment-based papers published. Hopefully this problem is now in the past, given that empirical/experimental papers are becoming more common.
Max Planck, one of the founders of quantum mechanics, found that physicists trained in what we now call classical physics, were not willing to teach or adopt a quantum mechanics world view; Planck observed: “Science advances one funeral at a time”.
Converting between IFPUG & COSMIC function point counts
Replication, repeating an experiment to confirm the results of previous experiments, is not a common activity in software engineering. Everybody wants to write about their own ideas and academic journals want to publish what is new (they are fashion driven).
Conversion between ways of counting function points, a software effort estimating technique, is one area where there has been a lot of replications (eight studies is a lot in software engineering, while a couple of hundred is a lot in psychology).
Amiri and Padmanabhuni’s Master’s thesis (yes, a thesis written by two people) lists data from 11 experiments where students/academics/professionals counted function points for a variety of projects using both the IFPUG and COSMIC counting methods. The data points are plotted below left and regression lines to each sample on the right (code+data):
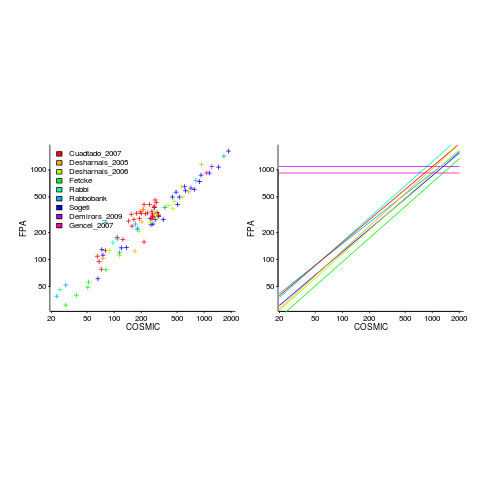
The horizontal lines are two very small samples where model fitting failed.
I was surprised to see such good agreement between different groups of counters. A study by Grimstad and Jørgensen asked developers to estimate effort (not using function points) for various projects, waited one month and repeated using what the developers thought were different projects. Most of the projects were different from the first batch, but a few were the same. The results showed developers giving completely different estimates for the same project! It looks like the effort invested in producing function point counting rules that give consistent answers and the training given to counters has paid off.
Two patterns are present in the regression lines:
- the slope of most lines is very similar, but they are offset from each other,
- the slope of some lines is obviously different from the others, with the different slopes all tilting further in the same direction. These cases mostly occur in the Cuadrado data (these three data sets are not included in the following analysis).
The kind of people doing the counting, for each set of measurements, is known and this information can be used to build a more sophisticated model.
Specifying a regression model to fit requires making several decisions about the kinds of uncertainty error present in the data. I have no experience with function points and in the following analysis I list the options and pick the one that looks reasonable to me. Please let me know if you have theory or data one suggesting what the right answer might be, I’m just juggling numbers here.
First we have to decide whether measurement error is additive or multiplicative. In other words, is there a fixed amount of potential error on each measurement, or is the amount of error proportional to the size of the project being measured (i.e., the error is a percentage of the total).
Does it make a difference to the fitted model? Sometimes it does and its always worthwhile to try building a model that mimics reality. If I tell you that 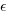 (Greek lower-case epsilon) is the symbol used to denote measurement error, you should be able to figure out which of the following two equations was built assuming additive/multiplicative error (confidence intervals have been omitted to keep things simple, they are given at the end of this post).
(Greek lower-case epsilon) is the symbol used to denote measurement error, you should be able to figure out which of the following two equations was built assuming additive/multiplicative error (confidence intervals have been omitted to keep things simple, they are given at the end of this post).
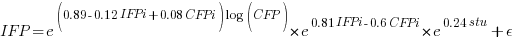
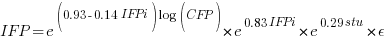
where: 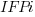 is 0 when the IFPUG counting is done by academics and 1 when done by industry,
is 0 when the IFPUG counting is done by academics and 1 when done by industry, 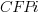 is 0 when the COSMIC counting is done by academics and 1 when done by industry,
is 0 when the COSMIC counting is done by academics and 1 when done by industry, 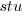 is 1 when the counting was done by students and 0 otherwise.
is 1 when the counting was done by students and 0 otherwise.
I think that measurement error is multiplicative for his problem and the remaining discussion is based on this assumption. Everything after the first exponential can be treated as effectively a constant, say 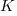 , giving:
, giving:
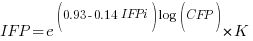
If we are only interested in converting counts performed by industry we get:
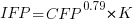
If we are using academic counters the equation is:
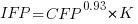
Next we have to decide where the uncertainty error resides. Nearly all forms of regression modeling assume that all the uncertainty resides in the response variable and that there is no uncertainty in the explanatory variables are measured without uncertainty. The idea is that the values of the explanatory variables are selected by the person doing the measurement, a handle gets turned and out pops the value of the response variable, plus error, for those particular, known, explanatory variable.
The measurements in this analysis were obtained by giving the subjects a known project specification, getting them to turn a handle and recording the function point count that popped out. So all function point counts contain uncertainty error.
Does the choice of response variable make that big a difference?
Let’s take the model fitted above and do some algebra to invert it, so that COSMIC is expressed in terms of IFPUG. We get the equation:
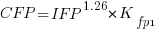
Now lets fit a model where the roles of response/explanatory variable are switched, we get:
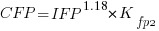
For this problem we need to fit a model that includes uncertainty in both variables containing function point counts. There are techniques for building models from scratch, known as errors-in-variables models. I like the SIMEX approach because it integrates well with existing R functionality for building regression models.
To use the simex function, from the R simex package, I have to decide how much uncertainty (in the form of a value for standard deviation) is present in the explanatory variable (the COSMIC counts in this case). Without any knowledge to guide the choice, I decided that the amount of error in both sets of count measurements is the same (a standard deviation of 3%, please let me know if you have a better idea).
The fitted equation for a model containing uncertainty in both counts is (see code+data for model details):
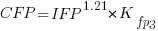
If I am interested in converting IFPUG counts to COSMIC, then what is the connection between the above model and reality?
I’m guessing that those most likely to perform conversions are in industry. Does this mean we can delete the academic subexpressions from the model, or perhaps fit a model that excludes counts made by academics? Is the Cuadrado data sufficiently different to be treated as an outlier than should be excluded from the model building process, or is it representative of an industry usage that does not occur in the available data?
There are not many industry only counts in the combined data. Perhaps the academic counters are representative of counters in industry that happen not to be included in the samples. We could build a mixed-effects model, using all the data, to get some idea of the variation between different sets of counters.
The 95% confidence intervals for the fitted exponent coefficient, using this data, is around 8%. So in practice, some of the subtitles in the above analysis are lost in the noise. To get tighter confidence bounds more data is needed.
Machine learning in SE research is a bigger train wreck than I imagined
I am at the CREST Workshop on Predictive Modelling for Software Engineering this week.
Magne Jørgensen, who virtually single handed continues to move software cost estimation research forward, kicked-off proceedings. Unfortunately he is not a natural speaker and I think most people did not follow the points he was trying to get over; don’t panic, read his papers.
In the afternoon I learned that use of machine learning in software engineering research is a bigger train wreck that I had realised.
Machine learning is great for situations where you have data from an application domain that you don’t know anything about. Lets say you want to do fault prediction but don’t have any practical experience of software engineering (because you are an academic who does not write much code), what do you do? Well you could take some source code measurements (usually on a per-file basis, which is a joke given that many of the metrics often used only have meaning on a per-function basis, e.g., Halstead and cyclomatic complexity) and information on the number of faults reported in each of these files and throw it all into a machine learner to figure the patterns and build a predictor (e.g., to predict which files are most likely to contain faults).
There are various ways of measuring the accuracy of the predictions made by a model and there is a growing industry of researchers devoted to publishing papers showing that their model does a better job at prediction than anything else that has been published (yes, they really do argue over a percent or two; use of confidence bounds is too technical for them and would kill their goose).
I long ago learned to ignore papers on machine learning in software engineering. Yes, sooner or later somebody will do something interesting and I will miss it, but will have retained my sanity.
Today I learned that many researchers have been using machine learning “out of the box”, that is using whatever default settings the code uses by default. How did I learn this? Well, one of the speakers talked about using R’s carat package to tune the options available in many machine learners to build models with improved predictive performance. Some slides showed that the performance of carat tuned models were often substantially better than the non-carat tuned model and many people in the room were aghast; “If true, this means that all existing papers [based on machine learning] are dead” (because somebody will now come along and build a better model using carat; cannot recall whether “dead” or some other term was used, but you get the idea), “I use the defaults because of concerns about breaking the code by using inappropriate options” (obviously somebody untroubled by knowledge of how machine learning works).
I think that use of machine learning, for the purpose of prediction (using it to build models to improve understanding is ok), in software engineering research should be banned. Of course there are too many clueless researchers who need the crutch of machine learning to generate results that can be included in papers that stand some chance of being published.
Computing academics destined to remain software engineering virgins
If you want to have a sensible conversation about software engineering with an academic, the best departments to search are Engineering and Physics (these days perhaps also Biology). Here you are much more likely to find people who have had to write large’ish programs to solve some research problem, than in the Computing department; they will understand what you are talking about because they have been there.
A lot of academics in Computing departments hold some seriously strange views about how non-trivial software engineering is done (but not the few who have actually written large programs). I recently had a moment of insight, these academics are treating the task of creating a large program as if it were just like coding up an algorithm, but bigger. I don’t know why I did not think of this before.
Does this insight have any practical use? Should I stop telling academics that algorithms are often not that important in solving a problem (I now understand why this comment baffles so many of them)?
Why don’t many computer science academics get involved in writing large programs? Its not an efficient use of their time (as more than one has explained to me); academics are rated by the number of papers they publish (plus the quality of the publishing journals and citations, etc) and the publishable paper/time ratio for large software development projects is not attractive for risk averse academics (which most of them are; any intrepid seekers of knowledge are soon hammered down by the bureaucracy, or leave for industry).
Recent Comments