Building a regression model is easy and informative
Running an experiment is very time-consuming. I am always surprised that people put so much effort into gathering the data and then spend so little effort analyzing it.
The Computer Language Benchmarks Game looks like a fun benchmark; it compares the performance of 27 languages using various toy benchmarks (they could not be said to be representative of real programs). And, yes, lots of boxplots and tables of numbers; great eye-candy, but what do they all mean?
The authors, like good experimentalists, make all their data available. So, what analysis should they have done?
A regression model is the obvious choice and the following three lines of R (four lines if you could the blank line) build one, providing lots of interesting performance information:
cl=read.csv("Computer-Language_u64q.csv.bz2", as.is=TRUE)
cl_mod=glm(log(cpu.s.) ~ name+lang, data=cl)
summary(cl_mod) |
The following is a cut down version of the output from the call to summary, which summarizes the model built by the call to glm.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.299246 0.176825 7.348 2.28e-13 ***
namechameneosredux 0.499162 0.149960 3.329 0.000878 ***
namefannkuchredux 1.407449 0.111391 12.635 < 2e-16 ***
namefasta 0.002456 0.106468 0.023 0.981595
namemeteor -2.083929 0.150525 -13.844 < 2e-16 ***
langclojure 1.209892 0.208456 5.804 6.79e-09 ***
langcsharpcore 0.524843 0.185627 2.827 0.004708 **
langdart 1.039288 0.248837 4.177 3.00e-05 ***
langgcc -0.297268 0.187818 -1.583 0.113531
langocaml -0.892398 0.232203 -3.843 0.000123 ***
Null deviance: 29610 on 6283 degrees of freedom
Residual deviance: 22120 on 6238 degrees of freedom
What do all these numbers mean?
We start with glm's first argument, which is a specification of the regression model we are trying to fit: log(cpu.s.) ~ name+lang
cpu.s. is cpu time, name is the name of the program and lang is the language. I found these by looking at the column names in the data file. There are other columns in the data, but I am running in quick & simple mode. As a first stab, I though cpu time would depend on the program and language. Why take the log of the cpu time? Well, the model fitted using cpu time was very poor; the values range over several orders of magnitude and logarithms are a way of compressing this range (and the fitted model was much better).
The model fitted is:
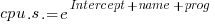 , or
, or 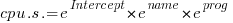
Plugging in some numbers, to predict the cpu time used by say the program chameneosredux written in the language clojure, we get: 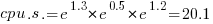 (values taken from the first column of numbers above).
(values taken from the first column of numbers above).
This model assumes there is no interaction between program and language. In practice some languages might perform better/worse on some programs. Changing the first argument of glm to: log(cpu.s.) ~ name*lang, adds an interaction term, which does produce a better fitting model (but it's too complicated for a short blog post; another option is to build a mixed-model by using lmer from the lme4 package).
We can compare the relative cpu time used by different languages. The multiplication factor for clojure is 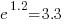 , while for
, while for ocaml it is 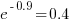 . So
. So clojure consumes 8.2 times as much cpu time as ocaml.
How accurate are these values, from the fitted regression model?
The second column of numbers in the summary output lists the estimated standard deviation of the values in the first column. So the clojure value is actually 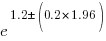 , i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the
, i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the ocaml values are 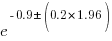 , between 0.3 and 0.6.
, between 0.3 and 0.6.
The fourth column of numbers is the p-value for the fitted parameter. A value of lower than 0.05 is a common criteria, so there are question marks over the fit for the program fasta and language gcc. In fact many of the compiled languages have high p-values, perhaps they ran so fast that a large percentage of start-up/close-down time got included in their numbers. Something for the people running the benchmark to investigate.
Isn't it easy to get interesting numbers by building a regression model? It took me 10 minutes, ok I spend a lot of time fitting models. After spending many hours/days gathering data, spending a little more time learning to build simple regression models is well worth the effort.
>> I am always surprised that people put so much effort into gathering the data and then spend so little effort analyzing it. <> This model assumes there is no interaction between program and language. <> In fact many of the compiled languages have high p-values, perhaps they ran so fast that a large percentage of start-up/close-down time got included in their numbers. Something for the people running the benchmark to investigate. <> Isn’t it easy to get interesting numbers by building a regression model? <<
Is it possible they are just bogus numbers, the result of a 10-minute bad-regression model?
"…where angels fear to tread."
https://www.poetryfoundation.org/articles/69379/an-essay-on-criticism
== I am always surprised that people put so much effort into gathering the data and then spend so little effort analyzing it. ==
Perhaps you don’t understand their goals?
== This model assumes there is no interaction between program and language. ==
What value analysis based on flawed assumptions?
== In fact many of the compiled languages have high p-values, perhaps they ran so fast that a large percentage of start-up/close-down time got included in their numbers. Something for the people running the benchmark to investigate. ==
Before speculating about “start-up/close-down time”, consider that the comparisons shown on the website only use measurements for the largest of the 3 workloads (column “n”).
== Isn’t it easy to get interesting numbers by building a regression model? ==
Is it possible they are just bogus numbers, the result of a 10-minute bad-regression model?
“…where angels fear to tread.”
https://www.poetryfoundation.org/articles/69379/an-essay-on-criticism
@Isaac Gouy
An odd collection of comments. The regression model is not bad or contain bogus numbers, but it is possible to draw bad conclusions from it. The most common ‘bad’ mistake is to generalize regression models to situations where they are not applicable.
The data used to build the model in this post is based on data obtained on a particular computing, running particular programs. The numbers would be different if a different computer were used (e.g., one whose memory had a different performance ratio to its cpu) and different programs. How big a difference would this make? I don’t know, but I would be wary of assuming too much.
1) What’s odd about suggesting an explanation for your surprise “that people put so much effort into gathering the data and then spend so little effort analyzing it” ?
For example, how would your regression model help with the goal — “To show working programs written in less familiar programming languages” ?
It wouldn’t — you simply don’t know the goals.
2) What’s odd about suggesting there may be little value in a model that’s based on such a flawed assumption ?
The reason you give for continuing is not that the model has any value, but that fixing the model would be “too complicated for a short blog post”.
3) What’s odd about suggesting there isn’t “something for the people running the benchmark to investigate” but there is something for you to investigate in your mis-use of their data ?
You tell us the model is based on a flawed assumption, you include data that “the people running the benchmark” exlude — and then tell us the “regression model is not bad or contain bogus numbers” !
“Don’t get your method advice from a method enthusiast. The best advice comes from people who care more about your problem than about their solution.” p115
https://books.google.com/books?id=pJ5QAAAAMAAJ