Cost/performance analysis of 1944-1967 computers: Knight’s data
Changes In Computer Performance and Evolving Computer Performance 1963-1967, by Kenneth Knight, are the references to cite when discussing the performance of early computers. I suspect that very few people have read the two papers they are citing (citing without reading is a surprisingly common practice). Both papers were published in Datamation, a computer magazine whose technical contents could rival that of the ACM journals in the 1960s, but later becoming more of a trade magazine. Until the articles appeared on bitsavers.org they were only really available through national or major regional libraries.
Both papers contain lots of interesting performance and cost data on computers going back to the 1940s. However, I was not interested enough to type in all that data. This week I found high quality OCRed copies of the papers on the Internet Archive; my effort was reduced to fixing typos, which felt like less work.
So let’s try to reproduce Knight’s analysis of the data (code and data). Working in the mid-1960s I imagine Knight did everything manually, with the help of mechanical calculators. I have the advantage of fancy software, a very fast computer and techniques that were invented after Knight did his analysis (e.g., generalized linear methods).
Each paper contains its own dataset: the first contains performance+cost data on 225 computers available between 1944 and 1963, while the second contains this information on 63 computers available between 1963 and 1967.
The dataset lists the computer name, the date it was introduced, number of operations per second and the number of seconds that can be rented for a dollar (most computer time used to be rented, then 25 years later personal computers came along and people got to own one, now 25 years after that Cloud is causing a switch back to rental per second).
How are operations measured? The MIPS unit of measurement did not start to be generally used until the 1980s. Knight used 30 or so system characteristics, such as time to perform various arithmetic operations and I/O time, plus characteristics of scientific and commercial applications to calculate a value considered to be a representative scientific or commercial operation.
There is no mention of how seconds-per-dollar values were obtained. Did Knight ask customers or vendors? In a rental market I imagine vendor pricing could be very flexible.
In the 1970s people started talking about Moore’s law, but in the 1960s there was Grosch’s law: Computer performance increases as the square of the cost, i.e., faster computers were cheaper to rent, for a given number of operations. Knight set out to empirically check Grosch’s law, i.e., he was looking for a quadratic fit.
Fitting a regression model to the 1950-1961 data, Knight obtained an exponent of 2.18, while I obtained 2.38 for commercial operations (using a slightly more sophisticated model, because I could); time on faster computers was cheaper than Grosch claimed. For scientific operations Knight obtained 1.92, while I obtained 3.56; despite trying all sorts of jiggery-pokery I could not get a lower value. Unless Knight used very different values to the ones published in the ‘scientific’ columns, one of us has made a big mistake (please let me know if my code is wrong).
Fitting a regression model to the 1963-1967 data, I get figures (both around 2.85 and 2.94) that are roughly in agreement with Knight (2.5 and 3.1). Grosch’s law has broken down by 1963 (if it ever held for scientific operations).
The plot below shows operations per second against operations per dollar for the 1953-1961 data, with fitted lines for some specific years. It shows that while customers get fewer seconds per dollar on faster computers, the number of operations performed in those seconds is raised to the power of two+.
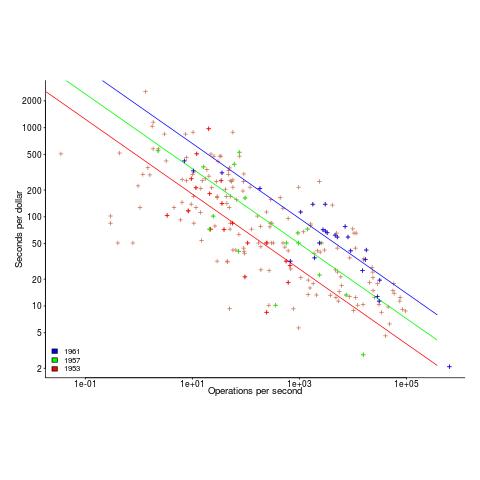
What other information can be extracted from the data? The 1953-1961 data shows seconds per dollar increased, over the whole performance range, by a factor of 1.15 per year, i.e., 15%, for both scientific and commercial; the 1963-1967 year on year increase jumps around a lot.
Recent Comments